题目内容
5.已知直角三角形的周长是2+$\sqrt{6}$,斜边长2,则这个直角三角形的面积为$\frac{1}{2}$.分析 设直角三角形的两直角边为a、b,根据题意和勾股定理得出a+b+2=2+$\sqrt{6}$,a2+b2=22=4,求出ab的值,即可求出答案.
解答 解:设直角三角形的两直角边为a、b,
则a+b+2=2+$\sqrt{6}$,a2+b2=22=4,
所以a+b=$\sqrt{6}$,(a+b)2-2ab=4,
解得:ab=1,
所以这个直角三角形的面积为$\frac{1}{2}$ab=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查了勾股定理和三角形的面积的应用,能根据已知和勾股定理求出ab的值是解此题的关键.

练习册系列答案
相关题目
20. 如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
 如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )
如图所示,有一“工”字形的机器零件,它是轴对称图形,图中所有的角都是直角,图中数据单位:cm,那么A.B两点之间的距离为( )| A. | 8cm | B. | 8$\sqrt{2}$cm | C. | 16cm | D. | 16$\sqrt{2}$cm |
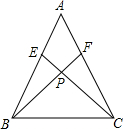 在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.
在△ABC中,AB=AC,点E,F分别在AB,AC上,AE=AF,BF与CE相交于点P.求证:△EBC≌△FCB.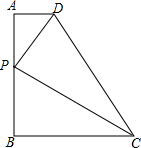 如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.
如图,已知直角梯形ABCD,∠A=∠B=90°,AD=2,BC=8,AB=10,在线段AB上取一点P,使△ADP与△BCP相似,求AP的长.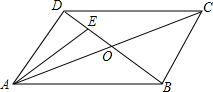 如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.
如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.