题目内容
4.在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,直线AD、CE交于点H,已知EH=EB=3,AE=4,则线段DH的长为$\frac{3}{5}$.分析 根据AD⊥BC,CE⊥AB,可得出∠EAH+∠B=90°∠EAH+∠AHE=90°,则∠B=∠AHE,则△AEH≌△CEB,从而得出CE=AE,根据已知条件得出CH的长,利用勾股定理求出AH的长,再通过证明△AEH∽△CDH,根据相似三角形的对应边比值相等即可求出DH的长.
解答 解:∵AD⊥BC,
∴∠EAH+∠B=90°,
∵CE⊥AB,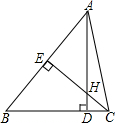
∴∠EAH+∠AHE=90°,
∴∠B=∠AHE,
∵EH=EB,
∴△AEH≌△CEB,
∴CE=AE,
∵EH=EB=3,AE=4,
∴CH=CE-EH=4-3=1,
∵∠AEH=∠CDH=90°,∠AHE=∠CHD,
∴△AEH∽△CDH,
∴$\frac{AH}{CH}=\frac{AE}{DH}$,
∵在Rt△AEH中,AH=$\sqrt{A{E}^{2}+E{H}^{2}}$=5,
∴$\frac{5}{1}$=$\frac{3}{DH}$,
∴DH=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质以及勾股定理的运用,根据同角的余角相等得出∠B=∠AHE,证明三角形全等进而求出CH=1,是解此题的关键.

练习册系列答案
相关题目
14.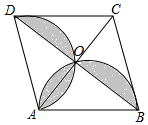 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,分别以AB、AD为直径作一个半圆,则图中阴影部分的面积为( )| A. | $\frac{25}{4}$π-12 | B. | $\frac{16}{3}$π-3 | C. | $\frac{9}{2}$π-6 | D. | $\frac{25}{8}$π-6 |
 如图,AD,AE分别是△ABC的高和中线,已知AD=5cm.EC=2cm.求△ABE和△AEC的面积.
如图,AD,AE分别是△ABC的高和中线,已知AD=5cm.EC=2cm.求△ABE和△AEC的面积.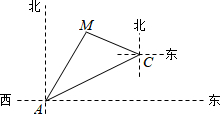 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西75°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求出管道MN的长度(精确到0.1米).
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西75°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求出管道MN的长度(精确到0.1米). 在等腰Rt△ABC中,AB=AC,∠DAE=45°,若BC=10,求BE•CD.
在等腰Rt△ABC中,AB=AC,∠DAE=45°,若BC=10,求BE•CD.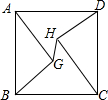 如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为2$\sqrt{2}$.
如图,正方形ABCD的边长为10,AG=CH=8,BG=DH=6,连接GH,则线段GH的长为2$\sqrt{2}$.