Question

9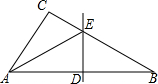．如图，在△ABC中，∠C=90°，∠B=30°，AB的垂直平分线分别交AB、BC于点D、E，若△ACE的周长为m，AB的长为n，则BC的长为m-$\frac{1}{2}$n．

Answer 1

分析 根据线段垂直平分线上的点到线段两端距离相等可得AE=BE，那么AC+CE+AE=AC+CE+BE=AC+BC=m．再根据直角三角形30°角所对的直角边等于斜边的一半可得AC=$\frac{1}{2}$AB=$\frac{1}{2}$n，那么BC=m-AC=m-$\frac{1}{2}$n．

解答 解：∵DE是AB的垂直平分线，
∴AE=BE，
∴AC+CE+AE=AC+CE+BE=AC+BC=m．
∵在△ABC中，∠C=90°，∠B=30°，
∴AC=$\frac{1}{2}$AB=$\frac{1}{2}$n，
∴BC=m-AC=m-$\frac{1}{2}$n．
故答案为m-$\frac{1}{2}$n．

点评 本题主要考查了垂直平分线的性质：角平分线上的点到角的两边距离相等的性质，直角三角形30°角所对的直角边等于斜边的一半的性质，熟记各性质是解题的关键．