题目内容
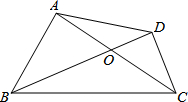如图，已知在四边形ABCD中，AC与BD相交于点O，AB⊥AC，CD⊥BD．（1）求证：△AOD∽△BOC；
（2）若cos∠ABO=
| ||
| 3 |
考点：相似三角形的判定与性质
专题：
分析：（1）由AB⊥AC，CD⊥BD，可得∠BAC=∠BDC=90°，又由对顶角相等，根据有两角对应相等的三角形相似，易得△AOB∽△DOC，即可得到比例线段，再由∠AOD=∠BOC，即可证得△AOD∽△BOC；
（2）由cos∠ABO=
，可得
=，又由相似三角形的面积比等于相似比的平方，可求得S△BOC的值．
（2）由cos∠ABO=
| ||
| 3 |
| AB |
| BO |
解答：（1）证明：∵AB⊥AC，CD⊥BD，
∴∠BAC=∠BDC=90°，
又∵∠AOB=∠DOC，
∴△AOB∽△DOC，
∴
=
∴
=
又∵∠AOD=∠BOC，
∴△AOD∽△BOC；
（2）∵∠BAC=90°，cos∠ABO=
，
∴
=
，
=
，
∵△AOD∽△BOC，
∴
=
，
∵S△BOC=18，
∴S△AOD=8．
∴∠BAC=∠BDC=90°，
又∵∠AOB=∠DOC，
∴△AOB∽△DOC，
∴
| AO |
| DO |
| BO |
| CO |
∴
| AO |
| BO |
| DO |
| CO |
又∵∠AOD=∠BOC，
∴△AOD∽△BOC；
（2）∵∠BAC=90°，cos∠ABO=
| ||
| 3 |
∴
| AB |
| BO |
| ||
| 3 |
| AO |
| BO |
| 2 |
| 3 |
∵△AOD∽△BOC，
∴
| S△AOD |
| S△BOC |
| 4 |
| 9 |
∵S△BOC=18，
∴S△AOD=8．
点评：此题考查了相似三角形的判定与性质，以及三角函数的定义．解题时要注意相似三角形的面积比等于相似比的平方，有两角对应相等的三角形相似与有两边对应成比例且夹角相等三角形相似的性质的应用．
练习册系列答案
相关题目
如图，E是平行四边形ABCD边BC上的一点，且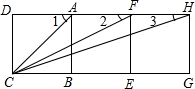
如图所示，三个边长为1个单位长度的正方形ABCD、ABEF、EFHG拼在一起．
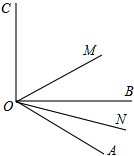如图，已知∠AOC与∠AOB的和为180度，OM，ON分别是∠AOC、∠AOB的平分线．