题目内容
13. 如图,在?ABCD中,∠C=108°,AE=AB,则∠ABE的度数是( )
如图,在?ABCD中,∠C=108°,AE=AB,则∠ABE的度数是( )| A. | 18° | B. | 36° | C. | 72° | D. | 108° |
分析 由平行四边形的性质和等腰三角形的性质即可得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴∠A=∠C=108°,
∵AE=AB,
∴∠ABE=∠AEB=$\frac{1}{2}$(180°-108°)=36°;
故选:B.
点评 本题主要考查平行四边形的性质、等腰三角形的性质以及三角形内角和定理;熟练掌握平行四边形的性质和等腰三角形的性质是解决问题的关键.

练习册系列答案
相关题目
18. 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
5.下列说法正确的是( )
| A. | 0没有平方根 | B. | -1的平方根是-1 | ||
| C. | 4的算术平方根是2 | D. | (-3)2的平方根是3 |
2.下列性质中,矩形具有但平行四边形不一定具有的是( )
| A. | 对边相等 | B. | 对角相等 | C. | 对角线相等 | D. | 对角线互相平分 |
 请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.
请仅用无刻度的直尺,作出下列各图中∠AOB的平分线,保留作图痕迹.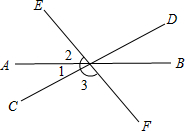 已知:如图,∠2=2∠1,∠3=3∠2,求∠DOE的度数.
已知:如图,∠2=2∠1,∠3=3∠2,求∠DOE的度数.