题目内容
 如图,已知△ABC≌△ADE,AD=AB,AE=AC,∠D-∠E=20°,∠BAC=60°,求∠C的度数.
如图,已知△ABC≌△ADE,AD=AB,AE=AC,∠D-∠E=20°,∠BAC=60°,求∠C的度数.考点:全等三角形的性质
专题:
分析:首先根据全等三角形的性质可得∠B=∠D,∠C=∠E,∠BAC=∠DAE,再根据∠BAC=60°,可得∠DAE=60°,根据三角形内角和定理可得∠D+∠E=120°,再加上条件∠D-∠E=20°,可计算出∠D=70°,∠E=50°,进而可得∠C的度数.
解答:解:∵△ABC≌△ADE,
∴∠B=∠D,∠C=∠E,∠BAC=∠DAE,
∵∠BAC=60°,
∴∠DAE=60°,
∴∠D+∠E=120°,
∵∠D-∠E=20°,
∴∠D=70°,∠E=50°,
∴∠C=50°,
故答案为:50°.
∴∠B=∠D,∠C=∠E,∠BAC=∠DAE,
∵∠BAC=60°,
∴∠DAE=60°,
∴∠D+∠E=120°,
∵∠D-∠E=20°,
∴∠D=70°,∠E=50°,
∴∠C=50°,
故答案为:50°.
点评:此题主要考查了全等三角形的性质,关键是掌握全等三角形对应角相等.

练习册系列答案
相关题目
以下是回收,绿色包装,节水,低碳四个标志,其中是轴对称图形的是( )
A、 |
B、 |
C、 |
D、 |
若(-x)2=(-5)2,则x的值为( )
| A、±5 | B、5 | C、-5 | D、25 |
 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=∠OAC,则∠AOC的大小是( )
如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC=∠OAC,则∠AOC的大小是( )| A、90° | B、45° |
| C、70° | D、60° |
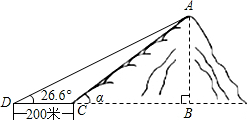 如图,小山岗的斜坡AC的坡度是
如图,小山岗的斜坡AC的坡度是 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是
如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长是