题目内容
6.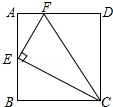 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;其中正确的结论是①③.(填写所有正确结论的序号)
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:①∠AEF=∠BCE;②AF+BC>CF;③S△CEF=S△EAF+S△CBE;其中正确的结论是①③.(填写所有正确结论的序号)
分析 延长CB,FE交于点G,易证∠AEF=∠BCE,可得①正确;即可证明△AEF≌△BEG,可得AF=BG,EF=EG,即可求得S△CEF=S△EAF+S△CBE,可得③正确;
可得AF+BC=CF,即可得②错误;
解答 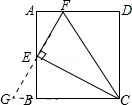 解:延长CB,FE交于点G,
解:延长CB,FE交于点G,
∵∠AEF+∠BEC=90°,∠BEC+∠BCE=90°,
∴∠AEF=∠BCE,①正确;
在△AEF和△BEG中,$\left\{\begin{array}{l}{∠FAE=∠GBE=90°}\\{AE=BE}\\{∠AEF=BEG}\end{array}\right.$,
∴△AEF≌△BEG(ASA),
∴AF=BG,EF=EG,
∵CE⊥EG,
∴S△CEG=S△CEF,CG=CF,
∴S△CEF=S△EAF+S△CBE,③正确;
∴AF+BC=BG+BC=CG=CF,②错误;
故答案为:①③.
点评 本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AEF≌△BEG和△CEF≌△CDF是解题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
1. 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
 如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
11.数据0,1,1,3,3,4的平均数和方差分别是( )
| A. | 2和1.6 | B. | 2和2 | C. | 2.4和1.6 | D. | 2.4和2 |