题目内容
 如图,在四边形ABCD中,∠BAD=90°,AB=BC=2,AC=2
如图,在四边形ABCD中,∠BAD=90°,AB=BC=2,AC=2| 3 |
| 3 |
考点:勾股定理,等腰三角形的性质,含30度角的直角三角形
专题:
分析:作辅助线构建直角三角形,可得∠DAE=60°,再根据含30度角的直角三角形的性质求出AF,DF的长,从而得到CF的长.根据勾股定理即可求出CD的长.
解答: 解:过B点作BE⊥AC于E,过D点作DF⊥AC于F,
解:过B点作BE⊥AC于E,过D点作DF⊥AC于F,
∵AB=BC=2,AC=2
,
∴cos∠BAE=
,即∠BAE=30°.
∵∠BAD=90°,
∴∠DAE=60°.
∵AD=
,
∴AF=
,DF=
,
∴CF=2
-
=
.
∴CD=
=3.
故答案为:3.
 解:过B点作BE⊥AC于E,过D点作DF⊥AC于F,
解:过B点作BE⊥AC于E,过D点作DF⊥AC于F,∵AB=BC=2,AC=2
| 3 |
∴cos∠BAE=
| ||
| 2 |
∵∠BAD=90°,
∴∠DAE=60°.
∵AD=
| 3 |
∴AF=
| ||
| 2 |
| 3 |
| 2 |
∴CF=2
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
∴CD=
| CF2+DF2 |
故答案为:3.
点评:本题考查了勾股定理、等腰三角形的性质、含30度角的直角三角形等知识.难度较大,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a3-a2=a |
| B、x6÷x2=x3 |
| C、(x3)2=x6 |
| D、a5•a2=a10 |
 如图所示,在直角坐标系中,矩形OABC的顶点B的坐标为(12,5),直线
如图所示,在直角坐标系中,矩形OABC的顶点B的坐标为(12,5),直线 如图是反比例函数
如图是反比例函数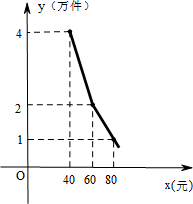 ,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
,该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示. 两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点.
两只大小不同的含45°角的三角板ABC和DBE如图摆放,直角顶点重合,连接AE,CD,F,M,N,G分别为线段AC,CD,ED,AE的中点. 如图,∠ABC=30°,BC=4,D是BC边的中点,E是边BA上一动点,则EC+ED的最小值是
如图,∠ABC=30°,BC=4,D是BC边的中点,E是边BA上一动点,则EC+ED的最小值是