题目内容
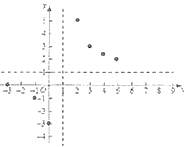
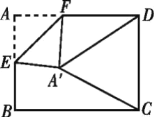
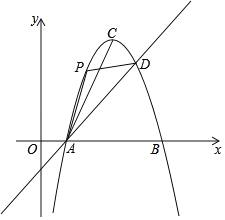
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 为坐标原点,且与反比例函数
为坐标原点,且与反比例函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,且
两点,且![]() 点的纵坐标为
点的纵坐标为![]() ,已知点
,已知点![]() ,则
,则![]() 的值为( ).
的值为( ).
A.![]() B.
B.![]() C.9D.
C.9D.![]()
【答案】D
【解析】
作AE⊥x轴交x轴于点E,作CF⊥x轴交x轴于点F,作BD∥x轴交AE于点D,证明△ADB≌△CFO,求出AD=CF=![]() ,同理证明△AEO≌△OFC,求出OF=AE=
,同理证明△AEO≌△OFC,求出OF=AE=![]() ,得到点C坐标即可解决问题.
,得到点C坐标即可解决问题.
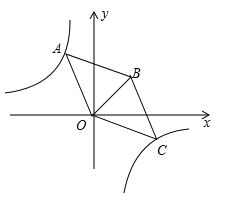
解:作AE⊥x轴交x轴于点E,作CF⊥x轴交x轴于点F,作BD∥x轴交AE于点D,

∵四边形AOCB是菱形,
∴AB∥CO,AB=CO,
∴∠ABO=∠COB,
又∵BD∥x轴,
∴∠DBO=∠FOB,
∴∠ABD=∠COF,
∵AD⊥BD,CF⊥OF,
∴∠ADB=∠CFO=90°,
又∵AB=CO,
∴△ADB≌△CFO(AAS),
∴AD=CF,
∵C点的纵坐标为![]() ,
,![]() ,
,
∴AD=CF=![]() ,
,
∴AE=![]() ,
,
同理可证,△AEO≌△OFC,
∴OF=AE=![]() ,
,
∴点C的坐标为(![]() ,
,![]() ),
),
∴k=![]() ,
,
故选:D.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
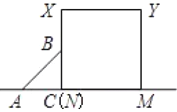
【题目】有这样一个问题:探究函数![]() 的图象与性质,小李根据学习函数的经验,对函数
的图象与性质,小李根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小李探究的过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是______;
的取值范围是______;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
则![]() 的值为_______;
的值为_______;
(3)如图所示,在平面直角坐标系![]() 中,根据描出的点,请补全此函数的图象;
中,根据描出的点,请补全此函数的图象;
(4)观察图象,写出该函数的一条性质_______;
(5)若函数![]() 的图象在函数
的图象在函数![]() 的图象上方,直接写出
的图象上方,直接写出![]() 的取值范围_______.
的取值范围_______.