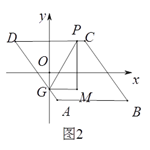题目内容
【题目】有这样一个问题:探究函数![]() 的图象与性质,小李根据学习函数的经验,对函数
的图象与性质,小李根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小李探究的过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是______;
的取值范围是______;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
则![]() 的值为_______;
的值为_______;
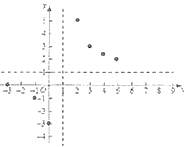
(3)如图所示,在平面直角坐标系![]() 中,根据描出的点,请补全此函数的图象;
中,根据描出的点,请补全此函数的图象;
(4)观察图象,写出该函数的一条性质_______;
(5)若函数![]() 的图象在函数
的图象在函数![]() 的图象上方,直接写出
的图象上方,直接写出![]() 的取值范围_______.
的取值范围_______.
【答案】(1)x≠1;(2)![]() ;(3)见解析;(4)当x>1或x<1时,y随x增大而减小;(5)-1<x<1或x>3.
;(3)见解析;(4)当x>1或x<1时,y随x增大而减小;(5)-1<x<1或x>3.
【解析】
(1)根据分式有意义分母不为零求解即可;
(2)把x=-2代入解析式计算即可;
(3)用平滑的曲线连接描出的点即可;
(4)根据函数图象可判断出增减性;
(5)画出两函数图象,根据图象写出x的取值范围即可.
解:(1)由题意得:x-1≠0,即x≠1,
故函数![]() 的自变量
的自变量![]() 的取值范围是x≠1;
的取值范围是x≠1;
(2)当x=-2时,![]() ,
,
即![]() ;
;
(3)函数图象如图所示:
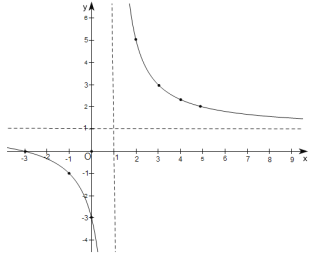
(4)由函数图象可知:当x>1或x<1时,y随x增大而减小;
(5)如图,函数![]() 的图象与函数
的图象与函数![]() 的图象的交点为(-1,-1),(3,3),
的图象的交点为(-1,-1),(3,3),
所以函数![]() 的图象在函数
的图象在函数![]() 的图象上方时,
的图象上方时,![]() 的取值范围为:-1<x<1或x>3.
的取值范围为:-1<x<1或x>3.


 单元期中期末卷系列答案
单元期中期末卷系列答案【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销![]() 件.已知产销两种产品的有关信息如下表:
件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(件) |
甲 | 6 |
| 20 | 200 |
乙 | 30 | 20 |
| 80 |
其中![]() 为常数,且
为常数,且![]() .
.
(1)若产销甲、乙两种产品的年利润分别为![]() 万元、
万元、![]() 万元,直接写出
万元,直接写出![]() 、
、![]() 与
与![]() 的函数关系式(写出自变量的取值范围);
的函数关系式(写出自变量的取值范围);
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.