题目内容
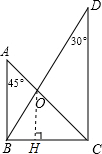
将一副三角板如图叠放，如OB=2| 3 |
考点：相似三角形的判定与性质
专题：
分析：根据题意得HO，BH的长，进而得出BC的长以及BD的长，即可得出DO的长．
解答：解：过点O作OH⊥BC于点H，
由题意可得：∠OBH=60°，
则sin60°=
=
，
解得：OH=3，
由BO=2
，可得BH=
，
∵∠A=∠ACB=45°，
∴HC=HO=3，
∴BC=
+3，
∵∠D=30°，
∴BD=2BC=6+2
，
∴DO=BC-BO=6．
故答案为：6．
由题意可得：∠OBH=60°，
则sin60°=
| OH |
| OB |
| ||
| 2 |
| OH | ||
2
|
解得：OH=3，
由BO=2
| 3 |
| 3 |
∵∠A=∠ACB=45°，
∴HC=HO=3，
∴BC=
| 3 |
∵∠D=30°，
∴BD=2BC=6+2
| 3 |
∴DO=BC-BO=6．
故答案为：6．
点评：本题考查了相似三角形的判定和性质以及解直角三角形，利用锐角三角函数的应用求出BC的长是解题关键．
练习册系列答案
相关题目
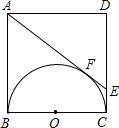在边长为a的正方形内ABCD中，AE与以BC为直径的半圆相切于点F，交CD于E，求CF、FD的长．
如图，在Rt△ABC中，BC=8，AC=6，∠ACB=90°，分别以A、B为圆心作两个外切的等圆，则图中阴影部分的面积是
如图，在四边形ABCD中，AD∥BC，∠BCD=90°，∠ABC=45°，AD=CD，CE平分∠ACB交AB于点E，在BC上截取BF=AE，连接AF交CE于点G，连接DG交AC于点H，过点A作AN⊥BC，垂足为N，AN交CE于点M．则下列结论：
如图，将△OAB绕点O沿顺时针方向旋转90°后得到△OA1B1，若OA=3，则AA1=
如图，在斜边为3的等腰直角三角形OAB中，作内接正方形A1B1C1D1；在等腰直角三角形OA1B1中，作内接正方形A2B2C2D2；在等腰直角三角形OA2B2中，作内接正方形A3B3C3D3…依次作下去，则第2014个正方形A2014B2014C2014D2014的边长是（ ）