题目内容
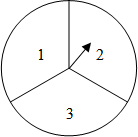如图，一个可以自由转动的转盘被等分成3个扇形区域，上面分别标有数字1、2、3．甲、乙两位同学用该转盘做游戏．（1）若转动该转盘1次，且规定：转盘停止转动时，指针指向区域的数字为奇数时甲获胜，否则乙获胜．记甲获胜的概率为P（甲），乙获胜的概率为P（乙），则P（甲）
（2）若两人各转动该转盘1次，且规定：游戏前每人各选定一个数字，如果两次转盘停止转动时，指针指向区域的数字之和与谁选的数字相同，则谁就获胜．在已知甲已选定数字3的情况下，乙为使自己获胜的概率比甲大，他应选择什么数字？试说明理由．
考点：列表法与树状图法
专题：
分析：（1）分别计算甲和乙的概率，比较大小即可；
（2）乙应选择数字4．用列表法得到两次指针指向区域数字的可能结果再分别计算其概率即可．
（2）乙应选择数字4．用列表法得到两次指针指向区域数字的可能结果再分别计算其概率即可．
解答：解：（1）∵P（甲）=
，P（乙）=
，
∴P（甲）＞P（乙），
故答案为：＞；
（2）乙应选择数字4．
理由如下：两次指针指向区域数字的可能结果如下：
以上共有9种可能的结果，且每种结果出现的可能性相同．
其中，出现数字之和为3的共有2种可能，即出现数字之和为3的概率P1=
；
出现数字之和为4的共有3种可能，即出现数字之和为4的概率P2=
．
∵P2＞P1，
∴乙选择数字4时获胜的概率比甲获胜的概率大．
| 2 |
| 3 |
| 1 |
| 3 |
∴P（甲）＞P（乙），
故答案为：＞；
（2）乙应选择数字4．
理由如下：两次指针指向区域数字的可能结果如下：
| 第1次 第2次 |
1 | 2 | 3 |
| 1 | （1，1） | （1，2） | （1，3） |
| 2 | （2，1） | （2，2） | （2，3） |
| 3 | （3，1） | （3，2） | （3，3） |
其中，出现数字之和为3的共有2种可能，即出现数字之和为3的概率P1=
| 2 |
| 9 |
出现数字之和为4的共有3种可能，即出现数字之和为4的概率P2=
| 1 |
| 3 |
∵P2＞P1，
∴乙选择数字4时获胜的概率比甲获胜的概率大．
点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．游戏双方获胜的概率相同，游戏就公平，否则游戏不公平．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
计算（-x）3•（-x）2的结果是（ ）
| A、x5 |
| B、-x5 |
| C、x6 |
| D、-x6 |
如图，已知∠1+∠2=180°，∠DAE=∠BCF．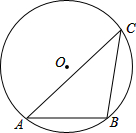
如图，圆O内接三角形△ABC．把△ABC以点O为旋转中心，顺时针方向旋转∠BOA的度数得到△EAF．