题目内容
16.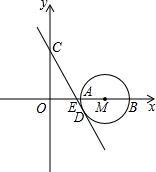 如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A,B.已知抛物线$y=\frac{1}{6}{x^2}+bx+c$过点A和B,与y轴交于点C.
如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A,B.已知抛物线$y=\frac{1}{6}{x^2}+bx+c$过点A和B,与y轴交于点C.(1)求抛物线的函数关系式并求点C的坐标.
(2)点Q(8,m)在抛物线$y=\frac{1}{6}{x^2}+bx+c$上,点P为此抛物线对称轴上一个动点,求PQ+PB最小值.
(3)CD是过点C的⊙M的切线,点D是切点,且与x轴交于点E,求切点D的坐标.
分析 (1)根据题意可知点A,B的坐标分别为(2,0),(6,0),代入函数解析式即可求得抛物线的解析式,即可得点C的坐标;
(2)根据图象可得PQ+PB的最小值即是AQ的长,所以抛物线对称轴l是x=4.所以Q(8,m)抛物线上,则m=2.过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,求的AQ的值即可;
(3)此题首先要证得OD∥CM,利用待定系数法求得CD的解析式,即可求得D点坐标.
解答 解:(1)由已知,得A(2,0),B(6,0),
∵抛物线y=$\frac{1}{6}$x2+bx+c过点A和B,
∴$\left\{\begin{array}{l}{\frac{1}{6}×{2}^{2}+2b+c=0}\\{\frac{1}{6}×{6}^{2}+6b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=-\frac{4}{3}}\\{c=2}\end{array}\right.$.
则抛物线的解析式为y=$\frac{1}{6}$x2-$\frac{4}{3}$x+2.
故C(0,2);
(2)如图①,抛物线对称轴l是x=4.
∵Q(8,m)在抛物线上,
∴m=2.过点Q作QK⊥x轴于点K,则K(8,0),QK=2,AK=6,
∴AQ=$\sqrt{A{K}^{2}+Q{K}^{2}}$=2$\sqrt{10}$.
又∵B(6,0)与A(2,0)关于对称轴l对称,
∴PQ+PB的最小值=AQ=2$\sqrt{10}$.
(3)如图②,连接DM和CM.
由已知,得DM=OC=2.
∵CD是⊙M的切线,
∴∠CDM=90°,
在△COE和△MDE中,
$\left\{\begin{array}{l}{∠COE=∠MDE}\\{∠CEO=∠MED}\\{OC=DM}\end{array}\right.$,
∴△DEM≌△DOC(AAS).
∴OE=DE,CE=ME.
设OE=x,CE=4x,由题意可得:x2+4=(4-x)2,
解得:x=$\frac{3}{2}$,
故E($\frac{3}{2}$,0),EM=$\frac{5}{2}$,
过点D作DH⊥x轴,设CD的函数表达式为:y=kx+2
将E($\frac{3}{2}$,0)代入得:
$\frac{3}{2}$k+2=0, 解得:k=-$\frac{4}{3}$,
解得:k=-$\frac{4}{3}$,
故CD的函数关系式为;y=-$\frac{4}{3}$x+2,
在△EDM中,AH×EM=ED×DM,
∵ED=$\frac{3}{2}$,DM=2,EM=$\frac{5}{2}$,
∴AD=$\frac{6}{5}$,则Dy=-$\frac{6}{5}$,
当y=-$\frac{6}{5}$时,
-$\frac{4}{3}$x+2=-$\frac{6}{5}$,
则-$\frac{4}{3}$x+2=-$\frac{6}{5}$,
解得:x=$\frac{12}{5}$,
故D($\frac{12}{5}$,-$\frac{6}{5}$).
点评 此题考查了二次函数与一次函数以及圆的综合知识,要注意待定系数法求解析式,要注意数形结合思想的应用.

| 售价x(元/件) | 100 | 105 | 110 | 115 | 120 |
| 销量y(件) | 60 | 50 | 40 | 30 | 20 |
 如图,A(5,0),B(3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(-4,0)出发,沿x轴向右以每秒2个单位长度的速度运动,运动时间t秒.
如图,A(5,0),B(3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°.点P从点Q(-4,0)出发,沿x轴向右以每秒2个单位长度的速度运动,运动时间t秒.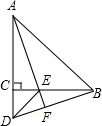 如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.
如图,△ABC、△ECD都是等腰直角三角形,且C在AD上.AE的延长线与BD交于F.请你猜想AE与BD的关系(数量关系和位置关系),并证明你的猜想.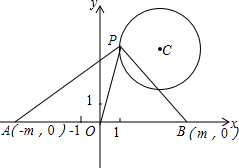 在平面直角坐标系xOy中,A(-m,0),B(m,0)(其中m>0),点P在以点C(3,4)为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,
在平面直角坐标系xOy中,A(-m,0),B(m,0)(其中m>0),点P在以点C(3,4)为圆心,半径等于2的圆上,如果动点P满足∠APB=90°,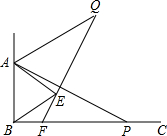 如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.
如图,已知∠ABC=90°,∠ABE是等边三角形,点P为射线BC上一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.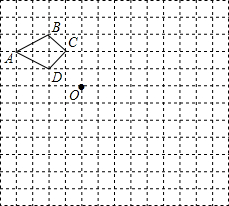 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网络线的交点)和点O,按要求画出四边形A1B1C1D1和四边形A2B2C2D2.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点四边形ABCD(顶点是网络线的交点)和点O,按要求画出四边形A1B1C1D1和四边形A2B2C2D2.