题目内容
1.在油箱汽油充足的情况下,轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系.已知某轿车油箱注满油后,以平均耗油量为0.1升/千米的速度行驶,可行驶800千米.(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式;
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
分析 (1)由轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系,可设S=$\frac{k}{a}$,再将a=0.1,S=800代入S=$\frac{k}{a}$,即可求得k的值,从而确定解析式;
(2)将a=0.08代入求得的函数的解析式即可求得S的值.
解答 解:(1)由题意可设S=$\frac{k}{a}$,
∵a=0.1,S=800,
∴800=$\frac{k}{0.1}$,
解得:k=80,
所以函数关系式为:S=$\frac{80}{a}$;
(2)将a=0.08代入S=$\frac{80}{a}$,
得:S=$\frac{80}{0.08}$=1000,
故该轿车可以行驶1000千米.
点评 本题考查了反比例函数的应用,解题的关键是从实际问题中抽象出反比例函数模型,然后利用待定系数法求出关系式.

练习册系列答案
相关题目
12.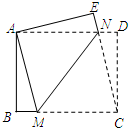 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,连结CN.若BM=1,BC=5,则MN的长为( )| A. | 2 | B. | 4 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{6}$ |
9.已知不等式mx+n>0的解集为x<2,则不等式(3m-n)x<2m+6n的解集是( )
| A. | x<-2 | B. | x>-2 | C. | x<14 | D. | x>14 |
10.已知?ABCD中,对角线AC、BD相交于点O,添加一个适当的条件,使?ABCD成为一个矩形.下列所加条件中,不符合要求的是( )
| A. | ∠ABC=90° | B. | AC=BD | C. | AC2=AB2+BC2 | D. | AC⊥BD |
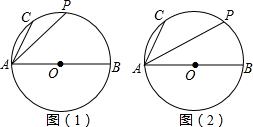
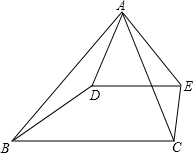 如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数. 如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,求作:
如图,已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$,$\overrightarrow{d}$,求作: