题目内容
6.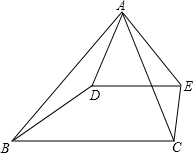 如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
如图,已知△ABD∽△ACE,∠ABC=50°,∠BAC=60°,求∠AED的度数.
分析 根据三角形内角和定理求出∠ACB=70°,根据相似三角形的性质得出$\frac{AB}{AC}$=$\frac{AD}{AE}$,∠BAD=∠CAE,求出$\frac{AB}{AD}$=$\frac{AC}{AE}$,∠BAC=∠DAE,推出△BAC∽△DAE,根据相似三角形的性质得出∠AED=∠ACB即可.
解答 解:∵∠ABC=50°,∠BAC=60°,
∴∠ACB=180°-∠ABC-∠BAC=70°,
∵△ABD∽△ACE,
∴$\frac{AB}{AC}$=$\frac{AD}{AE}$,∠BAD=∠CAE,
∴$\frac{AB}{AD}$=$\frac{AC}{AE}$,∠BAD+∠DAC=∠CAE+∠DAC,
∴∠BAC=∠DAE,
∴△BAC∽△DAE,
∴∠AED=∠ACB,
∴∠AED=70°.
点评 本题考查了相似三角形的性质和判定,三角形的内角和定理的应用,解此题的关键是求出△BAC∽△DAE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若不等式组$\left\{\begin{array}{l}{\frac{1}{3}x>1}\\{2-x≥a}\end{array}\right.$无解,则a的取值范围是( )
| A. | a>3 | B. | a≥-1 | C. | -1≤a<3 | D. | a≤-1 |
11.在坐标平面上两点A(-a+2,-b+1)、B(3a,b),若点A向右移动2个单位长度后,再向下移动3个单位长度后与点B重合,则点B所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.在平面直角坐标系中,点A,B的坐标分别为(-6,3),(-12,8),△ABO与△A′B′O是以原点O为位似中心得位似图形.若点A′的坐标为(2,-1),则点B′的坐标为( )
| A. | (-4,$\frac{8}{3}$) | B. | (4,-$\frac{8}{3}$) | C. | (-6,4) | D. | (6,-4) |
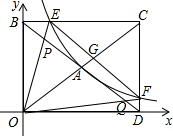 如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.
如图,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过矩形OBCD对角线的交点A,分别与CD、BC交于点F、点E,若三角形ODF的面积为2.