题目内容
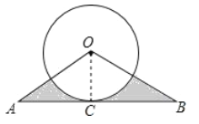
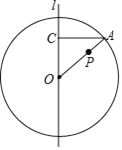
【题目】如图，定直线
经过圆心
，
是半径
上一动点，
于点
，当半径绕着点旋转时，总有
，若绕点旋转
时，、
两点的运动路径长的比值是__．
【答案】1．
【解析】
设⊙
的半径为R，
与⊙交于点B，由直角三角形的性质得出
,由已知得出
，证明△AOB是等边三角形，得出
，∠OPB=90°，得出点P在以OB为直径的圆上运动，圆心为C，由圆周角定理得出∠PCB=2∠AOB=120°，由弧长公式求出点A的路径长为
，点P的路径长为
，即可求出答案.
解：设⊙的半径为R，与⊙交于点B，连结AB,BP,PC,如图所示
∵
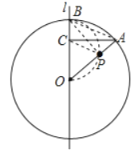
于点
，∠AOB=60°
∴∠OAC=30°
∴
∵OP=OC
∴
∵OA=OB,∠AOB=60°
∴△AOB是等边三角形
∴
∴∠OPB=90°
∴点P在以OB为直径的圆上运动，圆心为C
∴∠PCB=2∠AOB=120°
∴点A的路径长为，点P的路径长为
∴P，A两点的运动路径长的比值是1.
故答案为1.
练习册系列答案
相关题目
