Question

18．已知：△ABC为⊙O的内接三角形，AD⊥BC于D，AB=4，AC=3，AD=2，求⊙O的直径．

Answer 1

分析 首先连接AO交⊙O于E，连接BE，进而利用相似三角形的判定与性质得出$\frac{AB}{AD}$=$\frac{AE}{AC}$，求出即可．

解答 解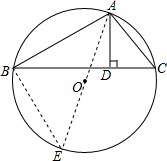：连接AO交⊙O于E，连接BE，
∵∠BEA与∠BCA都是AB边对应的圆周角，
∴∠BEA=∠BCA，
又∵AE是直径，
∴∠ABE=90°，
∵∠ADC=90°，
∴△ABE∽△ADC，
∴$\frac{AB}{AD}$=$\frac{AE}{AC}$，
则AE=$\frac{AB•AC}{AD}$=$\frac{4×3}{2}$=6，
即⊙O的直径为6．

点评 此题主要考查了相似三角形的判定与性质以及圆周角定理，得出△ABE∽△ADC是解题关键．