题目内容
10.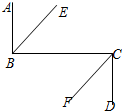 如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( )
如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么∠ABE与∠DCF的位置和大小关系是( )| A. | 是同位角且相等 | B. | 不是同位角但相等 | ||
| C. | 是同位角但不等 | D. | 不是同位角也不等 |
分析 根据∠ABC=∠DCB=90°,且∠EBC=∠BCF,运用等式性质得出∠ABE=∠DCF,再判断它们的位置即可.
解答 解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠EBC=∠BCF,
∴∠ABE=∠DCF,
∵∠ABE与∠DCF不在两直线的同侧,也不在第三条直线(截线)的同旁,
∴它们不是同位角.
故选(B)
点评 本题主要考查了平行线的性质以及同位角的识别,解题时注意:两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.

练习册系列答案
相关题目
6.(-0.25)2003×(-4)2002的值是( )
| A. | -0.25 | B. | 4 | C. | -4 | D. | -2 |
5.下列说法中正确的是( )
| A. | 在同一平面内,两条直线的位置只有两种:相交和垂直 | |
| B. | 如果两条直线都与第三条直线平行,那么这两条直线也互相平行 | |
| C. | 有且只有一条直线垂直于已知直线 | |
| D. | 从直线外一点到这条直线的垂线,叫做这点到这条直线的距离 |
2.下面说法正确的是 ( )
| A. | 绝对值最小的数是0 | B. | 绝对值相等的两个数相等 | ||
| C. | -a一定是负数 | D. | 有理数的绝对值一定是正数 |