Question

11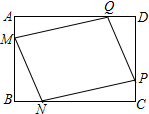．某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化，为了绿化环境又节省成本．如图，已知矩形的边BC=200m，边AB=a m（a为不大于200的常数），四边形MNPQ的顶点在矩形的边上，且AM=BN=CP=DQ=x m，设四边形MNPQ的面积为S m²
（1）求S关于x的函数关系式，并直接写出自变量x的取值范围；
（2）若a=120，求S的最小值，并求出此时x的值；
（3）若a=200，且每平方米绿化费用需50元，则此时绿化最低费用为100万元．

Answer 1

分析 （1）根据题意和图形可以得到S关于x的函数关系式和x的取值范围；
（2）根据a的值，将二次函数的一般形式化为顶点式，从而可以解答本题；
（3）根据a的值，将二次函数的一般形式化为顶点式，求出S的最小值，然后再乘以50，即可解答本题．

解答 解：（1）由题意可得，
S=200a-$\frac{x•（a-x）}{2}×2-\frac{（200-x）x}{2}×2$=2x²-（a+200）x+200a（0＜x＜a），
即S关于x的函数关系式是S=2x²-（a+200）x+200a，自变量x的取值范围是0＜x＜a；
（2）当a=120时，
S=2x²-320x+200×120=2（x-80）²+11200，
∴x=80时，S取得最小值，此时，S=11200，
即a=120，S的最小值是11200，此时x的值是80；
（3）当a=200时，
S=2x²-（200+200）x+200×200=2（x-100）²+20000，
∴当x=100时，S取得最小值，此时S=20000，
20000×50=1000000（元）=100（万元），
即此时绿化最低费用为100万元，
故答案为：100．

点评 本题考查二次函数的应用，解题的关键是明确题意，找出所求问题需要的条件，求出相应的二次函数的最值，注意第三问中要化为万元．