题目内容
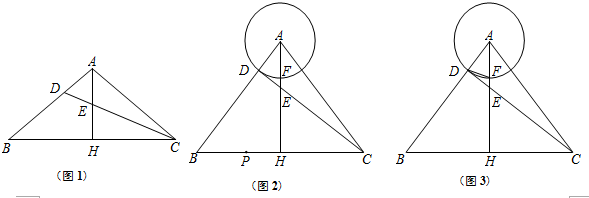
7.如图,已知在△ABC中,AB=AC=6,AH⊥BC,垂足为点H.点D在边AB上,且AD=2,联结CD交AH于点E.(1)如图1,如果AE=AD,求AH的长;
(2)如图2,⊙A是以点A为圆心,AD为半径的圆,交AH于点F.设点P为边BC上一点,如果以点P为圆心,BP为半径的圆与⊙A外切,以点P为圆心,CP为半径的圆与⊙A内切,求边BC的长;
(3)如图3,联结DF.设DF=x,△ABC的面积为y,求y关于x的函数解析式,并写出自变量x的取值范围.
分析 (1)如图1中,过点D作DG⊥AH于G,由DG∥BC得$\frac{AD}{AB}$=$\frac{DG}{BH}$=$\frac{DG}{HC}$=$\frac{ED}{EC}$=$\frac{EG}{EH}$=$\frac{1}{3}$,设EG=a,则EH=3a,列出方程即可解决.
(2)关键两个圆内切、外切半径之间的关系,先求出PH,设BP=x,根据AH2=AB2-BH2=AP2-PH2列出方程即可解决问题.
(3)如图3中过点D作DG⊥AF于G,设AG=t,根据AD2-AG2=DF2-FG2程即求出t与x的关系,再利用三角形面积公式计算即可.
解答 解:(1)如图1中,过点D作DG⊥AH于G,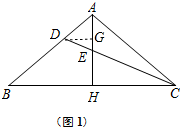
∵AH⊥BC,AB=AC
∴∠DGE=∠CHG=90°,BH=CH,
∴DG∥BC,
∴$\frac{AD}{AB}$=$\frac{DG}{BH}$=$\frac{DG}{HC}$=$\frac{ED}{EC}$=$\frac{EG}{EH}$=$\frac{1}{3}$,设EG=a,则EH=3a,
∴$\frac{AD}{BD}$=$\frac{AG}{GH}$=$\frac{1}{2}$,
∴AG=2a,AE=3a=2,
∴AH=6a=4.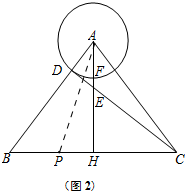
(2)如图2中,∵点P为圆心,BP为半径的圆与⊙A外切,CP为半径的圆与⊙A内切,
∴AP=AD+BP,AP=PC-AD,
∴AD+BP=PC-AD,
∴PC-BP=2AD=4,
∴PH+HC-(BH-PH)=4,
∴PH=2,
∵AH2=AB2-BH2=AP2-PH2,设BP=x,
∴62-(x+2)2=(x+2)2-22,
∴x=2$\sqrt{5}$-2,
∴BC=2BH=2(PB+PH)=4$\sqrt{5}$.
(3)如图3中,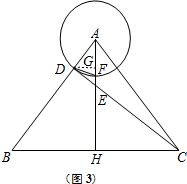 过点D作DG⊥AF于G,设AG=t,
过点D作DG⊥AF于G,设AG=t,
∵AD2-AG2=DF2-FG2,
∴22-t2=x2-(2-t)2,
∴t=$\frac{8-{x}^{2}}{4}$,
∴y=S△ABC=18•S△ADG=18×$\frac{1}{2}$•AG•DG=9•$\frac{8-{x}^{2}}{4}$•$\sqrt{{2}^{2}-(\frac{8-{x}^{2}}{4})^{2}}$,
∴y=$\frac{72x-9{x}^{3}}{16}$$\sqrt{16-{x}^{2}}$(0<x<2$\sqrt{2}$).
点评 本题考查圆的有关知识、两圆的位置关系、勾股定理、平行线分线段成比例定理等知识,解题的关键是用转化的思想,把问题掌握方程解决,属于中考参考题型.

| A. | a2-2ab-b2 | B. | a2+2ab+b2 | C. | a2-b2 | D. | a2-2ab+b2 |
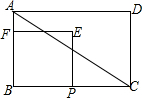 如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).
如图,在矩形ABCD中,AB=6,BC=8,点P从点B出发以每秒2个单位长度的速度向终点C运动,点P不与点B重合,以BP为边在BC上方作正方形BPEF,设正方形BPEF与△ABC的重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒).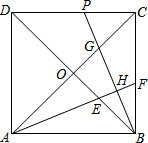 已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.
已知正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于点E、F,作BH⊥AF,垂足为H,BH的延长线分别交AC、CD于点G、P.