题目内容
A、B两地相距49千米,小彬步行从A地出发,分三段以不同的速度走完全程,共用10小时.已知第一段,第二段,第三段的速度分别是6千米/时,4千米/时,5千米/时,若各段路所用时间都是整数,求在每段路上所用时间.
考点:三元一次不定方程
专题:
分析:可设小彬在第一段上所用时间为a小时,在第二段上所用时间为b小时,在第三段上所用时间为c小时,根据等量关系:A、B两地相距49千米;共用10小时;列出方程组,再根据正整数的意义求解即可.
解答:解:设小彬在第一段上所用时间为a小时,在第二段上所用时间为b小时,在第三段上所用时间为c小时,依题意有
,
①-②×4,消去b,得c=9-2a③,
∵各段路所用时间都是整数,
∴a=1,b=2,c=7或a=2,b=3,c=5或a=3,b=4,c=3或a=4,b=5,c=1.
|
①-②×4,消去b,得c=9-2a③,
∵各段路所用时间都是整数,
∴a=1,b=2,c=7或a=2,b=3,c=5或a=3,b=4,c=3或a=4,b=5,c=1.
点评:考查了三元一次不定方程,此题是路程问题(路程=速度×时间),提高了学生的分析能力.解题关键是找到等量关系.

练习册系列答案
相关题目
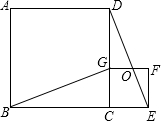 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b(a>b).下列结论:①△BCG≌△DCE;②BG⊥DE;③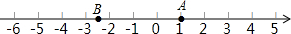 根据下面给出的数轴,解答下面的问题:
根据下面给出的数轴,解答下面的问题: 如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=
如图,正五边形ABCDE内接于圆O,对角线AC、BD交于点P,则∠APD=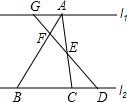 如图,l1∥l2,AF=
如图,l1∥l2,AF= 线段AC=8,点C是线段AB上一点,点D、E分别是线段AC,BC的中点,则线段DE的长
线段AC=8,点C是线段AB上一点,点D、E分别是线段AC,BC的中点,则线段DE的长 如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为
如图,⊙O的半径为4cm,∠AOB=60°,则弦AB的长为