题目内容
20．己知y＜$\sqrt{x-1}$+$\sqrt{1-x}$-2，请化简|3-x|+$\sqrt{{y}^{2}+4y+4}$．分析 根据二次根式的性质化简得出x的值以及y的取值范围，进而化简求出答案．
解答 解：∵y＜$\sqrt{x-1}$+$\sqrt{1-x}$-2，
∴x=1，y＜-2，
∴|3-x|+$\sqrt{{y}^{2}+4y+4}$
=2+$\sqrt{（y+2）^{2}}$，
=2-（y+2）
=-y．
点评 此题主要考查了二次根式的定义以及二次根式的性质与化简，正确得出x，y的取值是解题关键．
练习册系列答案
相关题目
2．在表中，我们把第i行第j列的数记为ai，j（其中i，j都是不大于3的正整数），对于表中的每个数ai，j规定如下：当i≥j时，ai，j=2i-j；当i＜j时，ai，j=i+3j．例如：当i=2，j=1时，ai，j=a2，1=3，按此规定，
（1）a1，3=10；
（2）表中这九个数的中位数是4；
（3）如果从表中这九个数中随机抽取一个数，那么抽到可能性最大的数是3；
（4）如果从表中这九个数中随机抽取一个数，那么抽到素数的概率是$\frac{2}{3}$．
（1）a1，3=10；
（2）表中这九个数的中位数是4；
（3）如果从表中这九个数中随机抽取一个数，那么抽到可能性最大的数是3；
（4）如果从表中这九个数中随机抽取一个数，那么抽到素数的概率是$\frac{2}{3}$．
| a1，1 | a1，2 | a1，3 |
| a2，1 | a2，2 | a2，3 |
| a3，1 | a3，2 | a3，3 |
19．
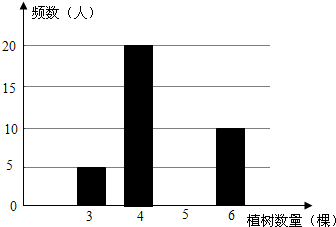学校组织师生开展植树造林活动，为了了解全校4000名学生的情况，随机抽样调查50名学生的植树情况，制成如下统计表和条形统计图（均不完整）．
（1）将统计表和条形统计图补充完整；
（2）求抽样的50名学生植树数量的平均数；
（3）根据抽样数据，估计该校4000名学生的植树数量．
学校组织师生开展植树造林活动，为了了解全校4000名学生的情况，随机抽样调查50名学生的植树情况，制成如下统计表和条形统计图（均不完整）．（1）将统计表和条形统计图补充完整；
（2）求抽样的50名学生植树数量的平均数；
（3）根据抽样数据，估计该校4000名学生的植树数量．
| 植树数量 （棵） | 频数 （人） | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | 0.4 |
| 5 | 15 | 0.3 |
| 6 | 10 | 0.2 |
| 合计 | 50 | 1 |
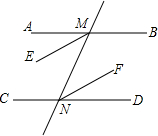如图，已知直线AB∥CD，直线MN分别交AB、CD于M、N两点，若ME、NF分别是∠AMN、∠DNM的角平分线，试说明：ME∥NF