题目内容
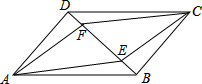 如图,已知在?ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )
如图,已知在?ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )| A、BE=DF |
| B、AF⊥BD,CE⊥BD |
| C、∠BAE=∠DCF |
| D、AF=CE |
考点:平行四边形的判定与性质
专题:
分析:连接AC与BD相交于O,根据平行四边形的对角线互相平分可得OA=OC,OB=OD,再根据对角线互相平分的四边形是平行四边形,只要证明得到OE=OF即可,然后根据各选项的条件分析判断即可得解.
解答: 解:如图,连接AC与BD相交于O,
解:如图,连接AC与BD相交于O,
在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB-BE=OD-DF,即OE=OF,故本选项错误;
B、若AF⊥BD,CE⊥BD,则可以利用“角角边”证明△ADF和△CBE全等,从而得到DF=BE,然后同A,故本选项错误;
C、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项错误;
D、AF=CE无法证明得到OE=OF,故本选项正确.
故选D.
 解:如图,连接AC与BD相交于O,
解:如图,连接AC与BD相交于O,在?ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB-BE=OD-DF,即OE=OF,故本选项错误;
B、若AF⊥BD,CE⊥BD,则可以利用“角角边”证明△ADF和△CBE全等,从而得到DF=BE,然后同A,故本选项错误;
C、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项错误;
D、AF=CE无法证明得到OE=OF,故本选项正确.
故选D.
点评:本题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定方法是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
对于反比例函数y=
,当自变量x的值从3增加到6时,函数值减少了1,则函数的解析式为( )
| k |
| x |
A、y=
| ||
B、y=
| ||
C、y=
| ||
D、y=
|
将两个全等的三角形(各边不相等,且无直角)按不同方式拼成的各种四边形中,四边形和平行四边形的个数分别为( )
| A、5,3 | B、5,4 |
| C、6,3 | D、6,4 |
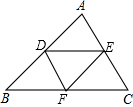 如图,在△ABC中,D,E,F分别在△ABC的三边上,且DE∥BC,DF∥AC,EF∥AB,则图中平行四边形有( )
如图,在△ABC中,D,E,F分别在△ABC的三边上,且DE∥BC,DF∥AC,EF∥AB,则图中平行四边形有( )| A、4个 | B、3个 | C、2个 | D、1个 |
如图,图①是一个水平摆放的小正方体木块,图②③是由这样的小正方体木块按一定的规律叠放而成的.其中图①的主视图有1个正方形,图②的主视图有4个正方形,图③的主视图有9个正方形,按照这样的规律继续叠放下去,则图⑩的主视图有正方形( )


| A、100个 | B、200个 |
| C、300个 | D、400个 |
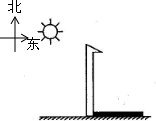 如图是王老师出示的他昨天画的一幅写生画,四个同学猜测他画这幅画的时间.请根据王老师给出的方向坐标,判断说的时间比较接近的是( )
如图是王老师出示的他昨天画的一幅写生画,四个同学猜测他画这幅画的时间.请根据王老师给出的方向坐标,判断说的时间比较接近的是( )| A、小丽说:“早上8时” |
| B、小强说:“中午12时” |
| C、小刚说:“下午5时” |
| D、小明说:“哪个时间段都行” |
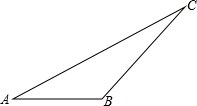 如图所示,已知在△ABC中,∠A=30°,∠B=135°,AC=8.求△ABC的面积.
如图所示,已知在△ABC中,∠A=30°,∠B=135°,AC=8.求△ABC的面积.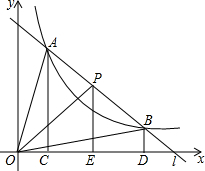 已知直线和双曲线交于A、B两点,P是线段AB上一点(P不与A、B重合),过点A、P、B分别向横坐标轴做垂线,垂足为C、D、E,连接OA、OB、OP,求证:S△POE>S△AOC=S△BOD.
已知直线和双曲线交于A、B两点,P是线段AB上一点(P不与A、B重合),过点A、P、B分别向横坐标轴做垂线,垂足为C、D、E,连接OA、OB、OP,求证:S△POE>S△AOC=S△BOD.