题目内容
将两个全等的三角形（各边不相等，且无直角）按不同方式拼成的各种四边形中，四边形和平行四边形的个数分别为（ ）
| A、5，3 | B、5，4 |
| C、6，3 | D、6，4 |
考点：平行四边形的判定,图形的剪拼
专题：
分析：三角形有三条边，三个内角，全等的三角形三个角三条边对应相等，则可以通过构造内错角使两边平行，同时由两边相等，根据平行四边形判定定理：一组对边平行且相等的四边形为平行四边形，得出结论．
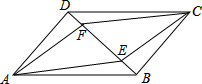
解答：
解：如图所示，由两个全等是三角形可以拼成四边形ADBC，四边形ABFC，四边形ABCE，四边形ACFD，四边形ABFE，四边形BCDE，其中四边形ADBC，四边形ABFC，四边形ABCE是平行四边形．
综上所述，将两个全等的三角形（各边不相等，且无直角）按不同方式拼成的各种四边形中，四边形和平行四边形的个数分别为6和3．
故选：C．
解：如图所示，由两个全等是三角形可以拼成四边形ADBC，四边形ABFC，四边形ABCE，四边形ACFD，四边形ABFE，四边形BCDE，其中四边形ADBC，四边形ABFC，四边形ABCE是平行四边形．综上所述，将两个全等的三角形（各边不相等，且无直角）按不同方式拼成的各种四边形中，四边形和平行四边形的个数分别为6和3．
故选：C．
点评：本题考查了平行四边形的判定以及全等三角形的性质．本题属于探究性试题，注意分情况讨论，不要丢一种情况．
练习册系列答案
阅读快车系列答案
相关题目
用公式法解方程x2-2=-3x时，a，b，c的值依次是（ ）
| A、0，-2，-3 |
| B、1，3，-2 |
| C、1，-3，-2 |
| D、1，-2，-3 |
将3x（a-b）-9y（b-a）因式分解，应提的公因式是（ ）
| A、3x-9y | B、3x+9y |
| C、a-b | D、3（a-b） |
电影院里座位呈阶梯形状或下坡形状的原因是（ ）
| A、增大盲区 |
| B、使盲区不变 |
| C、减小盲区 |
| D、为了美观而设计的 |
如图，C是线段AB上的一点，且AC：CB=2：3，那么AB：BC等于（ ）| A、2：3 | B、5：3 |
| C、3：2 | D、3：5 |
下列语句中不正确的是（ ）
| A、斜边和一锐角对应相等的两个直角三角形全等 |
| B、有两边对应相等的两个直角三角形全等 |
| C、有两个锐角相等的两个直角三角形全等 |
| D、有一直角边和一锐角对应相等的两个直角三角形全等 |
如图，已知在?ABCD中，E，F是对角线BD上的两点，则以下条件不能判断四边形AECF为平行四边形的是（ ）| A、BE=DF |
| B、AF⊥BD，CE⊥BD |
| C、∠BAE=∠DCF |
| D、AF=CE |