题目内容
3.已知α为锐角,sin(α+15°)=$\frac{\sqrt{3}}{2}$,计算$\sqrt{8}$-4cosα+tanα+$(\frac{1}{2})$-1的值.分析 先根据题意得出α的度数,再根据数的开方法则、特殊角的三角函数值及负整数指数幂分别计算出各数,再根据实数混合运算的法则进行计算即可.
解答 解:∵α为锐角,sin(α+15°)=$\frac{\sqrt{3}}{2}$,
∴α+15°=60°,即α=45°,
∴原式=2$\sqrt{2}$-4cos45°+tan45°+2
=2$\sqrt{2}$-4×$\frac{\sqrt{2}}{2}$+1+2
=2$\sqrt{2}$-2$\sqrt{2}$+1+2
=3.
点评 本题考查的是实数的运算,熟记特殊角的三角函数值是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列命题中,属于假命题的是( )
| A. | 等角的余角相等 | |
| B. | 在同一平面内垂直于同一条直线的两直线平行 | |
| C. | 相等的角是对顶角 | |
| D. | 有一个角是60°的等腰三角形是等边三角形 |
18.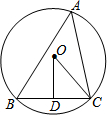 如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )
如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )
 如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )
如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠COD的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
 如图是由若干个边长为a的大小相同的小正方体组成的几何体,这个几何体的表面积是28a2.(用a的代数式表示)
如图是由若干个边长为a的大小相同的小正方体组成的几何体,这个几何体的表面积是28a2.(用a的代数式表示)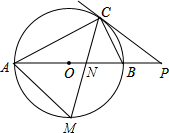 如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠ACB的平分线CM分别与AB,⊙O交于点N,M,且PC=PN.
如图,AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,∠ACB的平分线CM分别与AB,⊙O交于点N,M,且PC=PN. 如图,边长为a的大正方形内有一个边长为b的小正方形.
如图,边长为a的大正方形内有一个边长为b的小正方形. 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题: 如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
如图是每个面上都有一个汉字的正方体的一种展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )