题目内容
8. 如图,边长为a的大正方形内有一个边长为b的小正方形.
如图,边长为a的大正方形内有一个边长为b的小正方形.(1)用含字母的代数式表示图1中阴影部分的面积为a2-b2.
(2)将图1的阴影部分沿斜线剪开后,拼成了一个如图2所示的长方形,用含字母的代数式表示此长方形的长为a+b,宽为a-b,面积为(a+b)(a-b).
(3)比较(2)、(1)的结果,请你写出一个非常熟悉的公式(a+b)(a-b)=a2-b2.
(4)观察下列计算结果:
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…
用你发现的规律并结合(3)的公式,计算下面这个算式(用乘方的形式表示结果)并说出这个结果的个位数字.(2-1)(2+1)(22+1)(24+1)…(216+1)+1.
个位数字是:6.
分析 (1)求出大正方形及小正方形的面积,作差即可得出阴影部分的面积;
(2)图2所示的长方形的长和宽分别为(a+b)、(a-b),由此可计算出面积;
(3)根据阴影部分的面积相等可得出平方差公式;
(4)观察得出规律,即可解答.
解答 解:(1)图中阴影部分的面积是:a2-b2,
(2)长是 (a+b),宽是:a-b,长方形的面积是:(a+b)(a-b),
(3)(a+b)(a-b)=a2-b2
(4)原式=(22-1)(22+1)(24+1)…(216+1)+1
=(24-1)(24+1)…(216+1)+1
=(216-1)(216+1)+1
=(232-1)+1
=232
∵观察规律发现个位数字4个一组循环,
∴32÷4=8,
∴个位数字是:6.
点评 本题考查了平方差公式的应用,解此题的关键是能根据面积公式求出各个部分的面积,题型较好,难度适中,是一道不错的题目,通过此题能培养学生的观察能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列四组线段中,可以构成直角三角形的是( )
| A. | 4,5,6 | B. | 2,3,4 | C. | $\sqrt{7}$,3,4 | D. | 1,$\sqrt{2}$,3 |
 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为($\sqrt{3}$,0),直线L过点A(-$\sqrt{3}$,0),与⊙C相切于点D,求直线l的解析式.
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为($\sqrt{3}$,0),直线L过点A(-$\sqrt{3}$,0),与⊙C相切于点D,求直线l的解析式. 如图,点P是∠ABC内一点.
如图,点P是∠ABC内一点.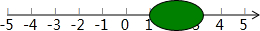 若将三个数$-\sqrt{3},\sqrt{6},\sqrt{10}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.
若将三个数$-\sqrt{3},\sqrt{6},\sqrt{10}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.