题目内容
2. 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若EF=8,则CD的长为8.
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若EF=8,则CD的长为8.
分析 根据三角形的中位线平行于第三边并且等于第三边的一半可得AB=2EF,再根据直角三角形斜边上的中线等于斜边的一半求解.
解答 解:∵E,F分别为AC,BC的中点,
∴EF是△ABC的中位线,
∴AB=2EF=2×8=16,
∵∠ACB=90°,点D是AB的中点,
∴CD=$\frac{1}{2}$AB=$\frac{1}{2}$×16=8.
故答案为:8.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,直角三角形斜边上的中线等于斜边的一半,熟记定理与性质是解题的关键.

练习册系列答案
相关题目
13.为了节约资源,科学指导居民改善居住条件,小强向房管部门提出了一个购买商品房的政策性方案:
设一个3口之家购买商品房的人均面积为x平方米,缴纳房款y万元.
(1)请求出y关于x的函数关系式;
(2)若某3人之家欲购买120平方米的商品房,求其应缴纳的房款.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米)部分 | 0.4 |
| 超过30平方米部分 | 0.9 |
(1)请求出y关于x的函数关系式;
(2)若某3人之家欲购买120平方米的商品房,求其应缴纳的房款.
11.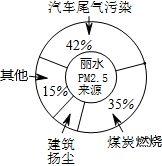 如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
 如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )
如图,是丽水PM2.5来源统计图,则根据统计图得出的下列判断中,正确的是( )| A. | 汽车尾气约为建筑扬尘的3倍 | B. | 表示建筑扬尘的占7% | ||
| C. | 表示煤炭燃烧的圆心角约126° | D. | 煤炭燃烧的影响最大 |
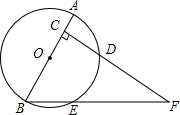 如图,己知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
如图,己知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
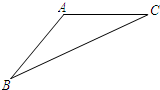 如图,△ABC中,AB=AC.
如图,△ABC中,AB=AC.