题目内容
8.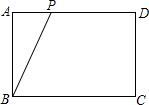 已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).
已知矩形ABCD中,AB=3cm,BC=4cm,一个动点P以1cm/s的速度从A点出发,沿AD,DC运动到C点,在这一过程中,运动时间x(s),P离D的距离为y(cm).(1)求y与x的函数关系,并写出自变量的取值范围;
(2)求当x=2,x=5时,y的值是多少?
(3)P点在AD上运动时,连接PB,当x为何值时PD=PB.
分析 (1)根据图形和点P的移动速度、方向确定P在不同线段上y与x的函数关系;
(2)把x的值代入相应的关系式求出y的值;
(3)根据勾股定理表示出PB的长,根据题意列出方程,解方程得到答案.
解答 解:(1)y=$\left\{\begin{array}{l}{4-x(0≤x≤4)}\\{x-4(4<x≤7)}\end{array}\right.$;
(2)当x=2时,y=2,
当x=5时,y=1;
(3)在Rt△APB中,AP=x,AB=3,
则PB=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{{x}^{2}+9}$,
当PD=PB时,$\sqrt{{x}^{2}+9}$=4-x,
解得,x=$\frac{7}{8}$.
点评 本题考查的是矩形的性质、列函数关系式和勾股定理的应用,正确理解题意、发现点P的移动方向和速度根据题意列出关系式是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
18.在0,2,-3,-$\frac{2}{3}$这四个数中,最大的数是( )
| A. | 0 | B. | 2 | C. | -3 | D. | -$\frac{2}{3}$ |
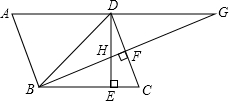 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
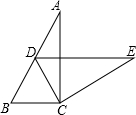 如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后
如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后