题目内容
6.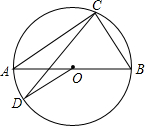 如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )
如图,AB是⊙O的直径,C、D是⊙O上的两点,分别连接AC、BC、CD、OD.若∠DOB=140°,则∠ACD=( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
分析 根据∠DOB=140°,求出∠AOD的度数,根据圆周角定理求出∠ACD的度数.
解答 解:∵∠DOB=140°,
∴∠AOD=40°,
∴∠ACD=$\frac{1}{2}$∠AOD=20°,
故选:A.
点评 本题考查的是圆周角定理,掌握一条弧所对的圆周角是这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
相关题目
16.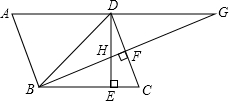 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
①BD=$\sqrt{2}$BE;②∠A=∠BHE;③CD2+BG2=AG2;④BH×DG=ED×GH.
正确的结论是( )
 在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:
在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,BF交DE于点H,交AD的延长线于点G,下面结论中:①BD=$\sqrt{2}$BE;②∠A=∠BHE;③CD2+BG2=AG2;④BH×DG=ED×GH.
正确的结论是( )
| A. | ①②③ | B. | ②③④ | C. | ①②④ | D. | ①②③④ |
1.据《梧州日报》报道,梧州黄埔化工药业有限公司位于万秀区松脂产业园,总投资119000000元,数字119000000用科学记数法表示为( )
| A. | 119×106 | B. | 11.9×107 | C. | 1.19×108 | D. | 0.119×109 |
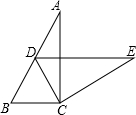 如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后
如图,在Rt△ABC中,∠ACB=90°,∠A=32°,将△ABC绕点C按顺时针方向旋转后