题目内容
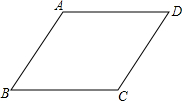 如图,在菱形ABCD中,AB=a,∠ABC=α.将菱形ABCD绕点B顺时针旋转(旋转角小于90°),点A、C、D分别落在A′、C′、D′处,当A′C′⊥BC时A′D=
如图,在菱形ABCD中,AB=a,∠ABC=α.将菱形ABCD绕点B顺时针旋转(旋转角小于90°),点A、C、D分别落在A′、C′、D′处,当A′C′⊥BC时A′D=考点:菱形的性质,旋转的性质
专题:
分析:当A′C′⊥BC时,D′在BC的延长线上,据此作出图形,利用三角函数求解.
解答: 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,
∴对角线AC⊥BD,
又∵A′C′⊥BC,
∴D′在BC的延长线上.
∵∠ABC=α,
∴BD=2a•cos
,
而A′D=BD-BA′=2a•cos
-a.
故答案是:2a•cos
-a.
 解:∵四边形ABCD是菱形,
解:∵四边形ABCD是菱形,∴对角线AC⊥BD,
又∵A′C′⊥BC,
∴D′在BC的延长线上.
∵∠ABC=α,
∴BD=2a•cos
| α |
| 2 |
而A′D=BD-BA′=2a•cos
| α |
| 2 |
故答案是:2a•cos
| α |
| 2 |
点评:本题考查了菱形的性质,根据菱形的性质,注意到D′和A′的位置,D′在BC的延长线上是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
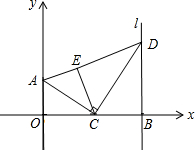 如图,点A的坐标是(0,2),点B是x轴正半轴上的点,过点B作直线l垂直于x轴,点C为线段OB上的动点,连接AC,过点C作CD⊥AC交直线l于点D,将△BCD沿CD翻折至△ECD的位置,连接AE,设点B的坐标是(m,0),点C的坐标是(n,0)
如图,点A的坐标是(0,2),点B是x轴正半轴上的点,过点B作直线l垂直于x轴,点C为线段OB上的动点,连接AC,过点C作CD⊥AC交直线l于点D,将△BCD沿CD翻折至△ECD的位置,连接AE,设点B的坐标是(m,0),点C的坐标是(n,0)
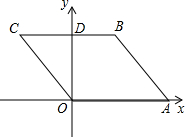 如图,菱形OABC的面积为
如图,菱形OABC的面积为