题目内容
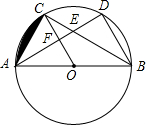 如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点.
如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为弧AD的中点.(1)求证:OF∥BD;
(2)若
| FE |
| ED |
| 1 |
| 2 |
考点:相似三角形的判定与性质,圆周角定理,扇形面积的计算
专题:
分析:(1)利用垂径定理的推论得出OC⊥AD,进而求出∠BDA=90°,BD⊥AD,进而得出答案;
(2)首先得出△ECF∽△EBD,进而得出FC=
BD,再得出△AOC为等边三角形,利用S阴影=S扇形AOC-S△AOC,求出即可.
(2)首先得出△ECF∽△EBD,进而得出FC=
| 1 |
| 2 |
解答:(1)证明:∵OC为半径,点C为弧AD的中点,
∴OC⊥AD.
∵AB为直径,
∴∠BDA=90°,BD⊥AD.
∴OF∥BD.
(2)解:∵点O为AB的中点,点F为AD的中点,∴OF=
BD.
∵FC∥BD,∴∠FCE=∠DBE.
∵∠FEC=∠DEB,∴△ECF∽△EBD,
∴
=
=
,∴FC=
BD.
∴FC=FO,即点F为线段OC的中点.
∵FC=FO,OC⊥AD,∴AC=AO,
又∵AO=CO,∴△AOC为等边三角形.
∴根据锐角三角函数定义,得△AOC的高为
×6=3
.
∴S阴影=
-
×6×3
=6π-9
(cm2).
答:图中阴影部分(弓形)的面积为(6π-9
)cm2.
∴OC⊥AD.
∵AB为直径,
∴∠BDA=90°,BD⊥AD.
∴OF∥BD.
(2)解:∵点O为AB的中点,点F为AD的中点,∴OF=
| 1 |
| 2 |
∵FC∥BD,∴∠FCE=∠DBE.
∵∠FEC=∠DEB,∴△ECF∽△EBD,
∴
| FC |
| BD |
| EF |
| ED |
| 1 |
| 2 |
| 1 |
| 2 |
∴FC=FO,即点F为线段OC的中点.
∵FC=FO,OC⊥AD,∴AC=AO,
又∵AO=CO,∴△AOC为等边三角形.
∴根据锐角三角函数定义,得△AOC的高为
| ||
| 2 |
| 3 |
∴S阴影=
| 60π×62 |
| 360 |
| 1 |
| 2 |
| 3 |
| 3 |
答:图中阴影部分(弓形)的面积为(6π-9
| 3 |
点评:此题主要考查了相似三角形的判定与性质以及扇形面积求法等知识,得出△ECF∽△EBD是解题关键.

练习册系列答案
相关题目
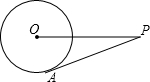 如图,P是⊙O外一点,PA是⊙O的切线,PO=13cm,PA=12cm,则⊙O的周长为( )
如图,P是⊙O外一点,PA是⊙O的切线,PO=13cm,PA=12cm,则⊙O的周长为( )| A、25πcm | B、5πcm |
| C、20πcm | D、10πcm |

 如图,一次函数y=-
如图,一次函数y=-
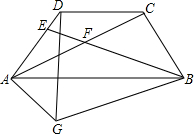 如图,AB∥CD,∠ABC=∠BAD=60°,连接AC,点E在AD上,连接BE,使∠ABE=∠CAD,BE交AC于F,将△ABE沿AB翻折得△ABG,点E落在点G处,连接DG.若EF=
如图,AB∥CD,∠ABC=∠BAD=60°,连接AC,点E在AD上,连接BE,使∠ABE=∠CAD,BE交AC于F,将△ABE沿AB翻折得△ABG,点E落在点G处,连接DG.若EF=