��Ŀ����
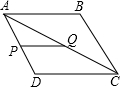
6����ͼ1������ABCD�У�AB=2$\sqrt{3}$��BC=6����P��Q�ֱ����߶�AD���߶�BC�ϵĶ��㣬�����PQB=60�㣮��1����գ��١�ACB=30�ȣ���PQ=4��
��2�����߶�BC���е�ΪN��PQ���߶�AC�ཻ�ڵ�M������CMNΪֱ�������Σ���ֱ��д������������AP�ij��ȣ�
��3����AP=x����PBQ���ABC���ص����ֵ����ΪS������S��x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
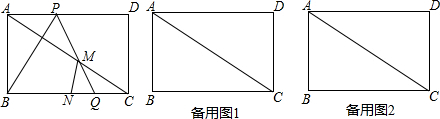
���� ��1�����ɾ��ε����ʵó���ABC=90�㣬�������Ǻ����Ķ���ó�tan��ACB=$\frac{AB}{BC}$=$\frac{\sqrt{3}}{3}$�����ɵó������ ����PG��BC��G�������Ǻ������PQ���ɣ�
��2����AP=x��������������ٵ���NMC=90��ʱ�������CN=$\frac{1}{2}$BC=3����������ó���PAM=��PMA=��QMC=��QCM=30�㣬��MNQ=��MQN=60�㣬�ó�PM=AP=x��MQ=4-x��MN=$\frac{3}{2}$��MN=MQ���ó�4-x=$\frac{3}{2}$���ⷽ�̼��ɣ��ڵ���MNC=90��ʱ���ӳ�NM��AD��H����Rt��PMH�У�PM=2��HM=$\sqrt{3}$����PH=1���ó�AP=AH-PH=2��
��3������PC����֤����APE�ס�CBE���ó�����ʽ�������BEC��������������PQC������͡�CMQ�������S�ı���BQME=S��BEC-S��CMQ�����ɵó��������P��A�غ�ʱ��x=0����Q��C�غ�ʱ��x=4�����ɵó�x��ȡֵ��Χ��
��� �⣺��1���١��ı���ABCD�Ǿ��Σ�
���ABC=��D=90�㣬AD=BC=6��AD��BC��
��tan��ACB=$\frac{AB}{BC}$=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$��
���ACB=30�㣬
�ʴ�Ϊ��30��
����PG��BC��G����ͼ1��ʾ��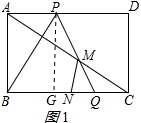 ���PGC=90�㣬PG=AB=2$\sqrt{3}$��
���PGC=90�㣬PG=AB=2$\sqrt{3}$��
��PQ=$\frac{PG}{sin��PQB}$=$\frac{2\sqrt{3}}{\frac{\sqrt{3}}{2}}$=4��
�ʴ�Ϊ��4��
��2����AP=x�������������
�ٵ���NMC=90��ʱ����ͼ1��ʾ��
��N��BC���е㣬
��CN=$\frac{1}{2}$BC=3��
��������ã���PAM=��PMA=��QMC=��QCM=30�㣬��MNQ=��MQN=60�㣬
��PM=AP=x��MQ=4-x��MN=$\frac{3}{2}$��MN=MQ��MN=$\frac{1}{2}$CN=$\frac{3}{2}$��
��4-x=$\frac{3}{2}$��
��ã�x=$\frac{5}{2}$��
��PA=$\frac{5}{2}$��
�ڵ���MNC=90��ʱ��
�ӳ�NM��AD��H����ͼ2��ʾ��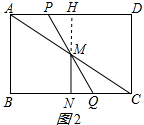 ��Rt��PMH�У�PM=2��HM=$\sqrt{3}$����PH=1��
��Rt��PMH��PM=2��HM=$\sqrt{3}$����PH=1��
��AP=AH-PH=2��
������������CMNΪֱ�������Σ�AP�ij���Ϊ��$\frac{5}{2}$��2��
��3����PB��AC��E������PC����ͼ3��ʾ��
��AD��BC��
���APE�ס�CBE��
��$\frac{CE}{AE}=\frac{BC}{AP}=\frac{6}{x}$��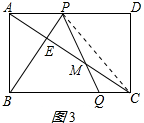
��$\frac{CE}{AC}=\frac{6}{x+6}$��
��S��BEC=$\frac{6}{x+6}$•S��ABC=$\frac{6}{x+6}$��$\frac{1}{2}$��6��2$\sqrt{3}$=$\frac{36\sqrt{3}}{x+6}$��
��PM=PA=x��
��CQ=QM=4-x��
��S��PQC=$\frac{1}{2}��4-x��•2\sqrt{3}=\sqrt{3}��4-x��$��
��S��CMQ=$\frac{QM}{PQ}$•S��PQC=$\frac{4-x}{4}$•S��PQC=$\frac{4-x}{4}$•$\sqrt{3}$��4-x��=$\frac{\sqrt{3}}{4}$��4-x��2��
��S�ı���BQME=S��BEC-S��CMQ=$\frac{{36\sqrt{3}}}{x+6}-\frac{{\sqrt{3}}}{4}{��4-x��^2}$��
��P��A�غ�ʱ��x=0��
��Q��C�غ�ʱ��PD=2��
��AP=4����x=4��
���Ա���x��ȡֵ��Χ�ǣ�0��x��4��
��S=$\frac{{36\sqrt{3}}}{x+6}-\frac{{\sqrt{3}}}{4}{��4-x��^2}$��0��x��4����
���� �������ı����ۺ���Ŀ�������˾��ε����ʡ����Ǻ��������������ε��ж������������ε��ж��������Լ�����������ļ����֪ʶ�������ѶȽϴ��ۺ���ǿ���ر��ǣ�2����3���У���Ҫͨ���������ߣ����з������ۻ�֤�����������Ʋ��ܵó������

 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�| A�� | ��2x2��3=8x6 | B�� | 5a2b-2a2b=3 | C�� | x6��x2=x3 | D�� | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ |
| A�� | x2=1 | B�� | ��x+1��2=0 | C�� | x2+1=0 | D�� | 2��x+1��=0 |
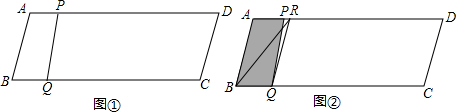
 ��ͼ��������ABCD�У�P��Q�ֱ���AD��AC���е㣬���PQ=3����ô����ABCD���ܳ��ǣ�������
��ͼ��������ABCD�У�P��Q�ֱ���AD��AC���е㣬���PQ=3����ô����ABCD���ܳ��ǣ�������| A�� | 30 | B�� | 24 | C�� | 18 | D�� | 6 |
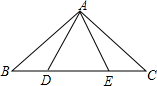 ��ͼ����B��D��E��C��һ��ֱ���ϣ���ABD�ա�ACE��AB��AC��AD��AE�Ƕ�Ӧ�ߣ�����ABD�ա�ACE�⣬ͼ�л�������ȫ�������������У���д��������֤����Ľ��ۣ�
��ͼ����B��D��E��C��һ��ֱ���ϣ���ABD�ա�ACE��AB��AC��AD��AE�Ƕ�Ӧ�ߣ�����ABD�ա�ACE�⣬ͼ�л�������ȫ�������������У���д��������֤����Ľ��ۣ�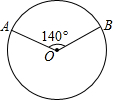 ��ͼ��A��B�ǡ�O�����㣬��AOB=140�㣬P�ǡ�O�ϵ�һ�����㣬P�����A��B�غϣ����APB=70���110�㣮
��ͼ��A��B�ǡ�O�����㣬��AOB=140�㣬P�ǡ�O�ϵ�һ�����㣬P�����A��B�غϣ����APB=70���110�㣮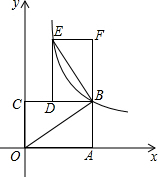 ��ͼ������OABC������OA��OC�ֱ���x��y����������ϣ���B������Ϊ��3��2��������������y=$\frac{k}{x}$��k��0��x��0����ͼ����B��
��ͼ������OABC������OA��OC�ֱ���x��y����������ϣ���B������Ϊ��3��2��������������y=$\frac{k}{x}$��k��0��x��0����ͼ����B��