题目内容
 如图,在?ABCD中,E,F分别是AB,CD的中点,G,H分别是AF,CE的中点,连结EG,FH.
如图,在?ABCD中,E,F分别是AB,CD的中点,G,H分别是AF,CE的中点,连结EG,FH.(1)四边形EHFG是不是平行四边形?如果是,请给出证明;如果不是,请说明理由;
(2)求四边形EHFG的面积与平行四边形ABCD的面积之比.
考点:平行四边形的判定与性质
专题:计算题
分析:(1)四边形EHFG为平行四边形,理由为:由四边形ABCD为平行四边形得到DC与AB平行且相等,而E、F分别为AB、CD的中点,得到FC与AE平行且相等,即四边形AECF为平行四边形,可得出GF与HE平行,再由G、H分别为AF与CE中点,得到GF=HE,即可得到四边形GEHF为平行四边形;
(2)由E、F分别为AB、CD的中点,得到四边形AECF的面积=三角形ADF面积+三角形EBC面积=
平行四边形ABCD面积,作FJ垂直与CE,FJ为四边形EHFG及四边形AECF的高,求出四边形EHFG面积与四边形AECF面积之比,即可确定出四边形EHFG的面积与平行四边形ABCD的面积之比.
(2)由E、F分别为AB、CD的中点,得到四边形AECF的面积=三角形ADF面积+三角形EBC面积=
| 1 |
| 2 |
解答: 解:(1)四边形EHFG为平行四边形,理由为:
解:(1)四边形EHFG为平行四边形,理由为:
∵ABCD为平行四边形,
∴DC∥AB,DC=AB,
∵E、F分别为AB、CD的中点,
∴DF=CF=
DC,AE=BE=
AB,
∴FC=AE,
∵FC∥AE,
∴四边形AECF为平行四边形,
∴AF∥EC,且AF=EC,
∵G、H分别为AF、CE的中点,
∴GF=EH,
则四边形EHFG为平行四边形;
(2)∵E、F为AB、CD的中点,
∴S四边形AECF=S△ADF+S△EBC(底乘高可算得),即S平行四边形AECF:S平行四边形ABCD=1:2,
过F做FJ⊥CE于J点,FJ为四边形EHFG及四边形AECF的高,
又∵G、H为中点,
∴S四边形EHFG:S四边形AECF=1:2(FJ•EC=FJ•2•EH),则S四边形EHFG:S四边形ABCD=1:4.
 解:(1)四边形EHFG为平行四边形,理由为:
解:(1)四边形EHFG为平行四边形,理由为:∵ABCD为平行四边形,
∴DC∥AB,DC=AB,
∵E、F分别为AB、CD的中点,
∴DF=CF=
| 1 |
| 2 |
| 1 |
| 2 |
∴FC=AE,
∵FC∥AE,
∴四边形AECF为平行四边形,
∴AF∥EC,且AF=EC,
∵G、H分别为AF、CE的中点,
∴GF=EH,
则四边形EHFG为平行四边形;
(2)∵E、F为AB、CD的中点,
∴S四边形AECF=S△ADF+S△EBC(底乘高可算得),即S平行四边形AECF:S平行四边形ABCD=1:2,
过F做FJ⊥CE于J点,FJ为四边形EHFG及四边形AECF的高,
又∵G、H为中点,
∴S四边形EHFG:S四边形AECF=1:2(FJ•EC=FJ•2•EH),则S四边形EHFG:S四边形ABCD=1:4.
点评:此题考查了平行四边形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
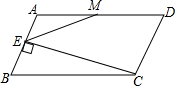 如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.
如图,在?ABCD中,AD=2CD,M是AD的中点,CE⊥AB于点E,连结EM.求证:∠DME=3∠AEM.
 如图,在?ABCD中,延长AD到点E,使得DE=AD,连结BE.求证:CD与BE互相平分.
如图,在?ABCD中,延长AD到点E,使得DE=AD,连结BE.求证:CD与BE互相平分. 如图,已知CD垂直平分AB,AB平分∠CAD.求证:AD∥BC.
如图,已知CD垂直平分AB,AB平分∠CAD.求证:AD∥BC. 如图,已知△ABC,求作正方形DEFG,使DE在边BC上,点G,F分别在AB,AC上.
如图,已知△ABC,求作正方形DEFG,使DE在边BC上,点G,F分别在AB,AC上. 如图,在△ABC中,∠=90°,AC=2
如图,在△ABC中,∠=90°,AC=2