题目内容
 如图,已知DE∥AB,BD平∠ABC分,∠1=∠2,求证:EF平分∠CED.
如图,已知DE∥AB,BD平∠ABC分,∠1=∠2,求证:EF平分∠CED.考点:平行线的判定与性质
专题:证明题
分析:根据同位角相等,两直线平行由∠1=∠2得到BD∥EF,则根据平行线的性质得∠BDE=∠DEF,再由DE∥AB得∠BDE=∠ABD,所以∠ABD=∠DEF,根据角平分线的性质得∠1=∠ABD,则∠1=∠DEF,加上∠1=∠2,于是得到∠2=∠DEF.
解答:证明:∵∠1=∠2,
∴BD∥EF,
∴∠BDE=∠DEF,
∵DE∥AB,
∴∠BDE=∠ABD,
∴∠ABD=∠DEF,
∵BD平分∠ABC,
∴∠1=∠ABD,
∴∠1=∠DEF,
而∠1=∠2,
∴∠2=∠DEF,
即EF平分∠CED.
∴BD∥EF,
∴∠BDE=∠DEF,
∵DE∥AB,
∴∠BDE=∠ABD,
∴∠ABD=∠DEF,
∵BD平分∠ABC,
∴∠1=∠ABD,
∴∠1=∠DEF,
而∠1=∠2,
∴∠2=∠DEF,
即EF平分∠CED.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,内错角相等.

练习册系列答案
相关题目
 如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.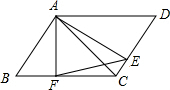 如图,平行四边形ABCD中,AF⊥BC于点F,AE⊥CD于点E,连接AC、FE.求证:AC•AF=EF•AB.
如图,平行四边形ABCD中,AF⊥BC于点F,AE⊥CD于点E,连接AC、FE.求证:AC•AF=EF•AB.