Question

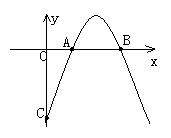
如图,已知抛物线y=-x²+bx+c与x轴的两个交点分别为A(x₁,0),B(x₂,0) , 且x₁+x₂=4, 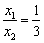.(1)求抛物线的代数表达式;

    (2)设抛物线与y轴交于C点,求直线BC的表达式;

    (3)求△ABC的面积.

 

Answer 1

(1)解方程组, 得x₁=1,x₂=3

    故 ,解这个方程组,得b=4,c=-3.

    所以,该抛物线的代数表达式为y=-x²+4x-3.

    (2)设直线BC的表达式为y=kx+m.

    由(1)得,当x=0时,y=-3,故C点坐标为(0,-3).

    所以, 解得

    ∴直线BC的代数表达式为y=x-3

    (3)由于AB=3-1=2,OC=│-3│=3.

    故S_△ABC=AB·OC=×2×3=3.