Question

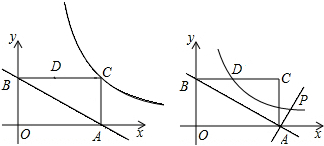
如图，在平面直角坐标系中，直线y=-

1

2

x+b（b＞0）分别交x轴，y轴于A、B两点，以OA、OB为边作矩形OACB，D为BC的中点．当b=

6

时，点C在函数y=

k

x

的图象上．
（1）求该函数的解析式；
（2）当b=

5

2

时，过点A作AB的垂线与函数y=

k

x

的图象在第一象限内的交点为P，求点P的坐标；
（3）在b值的变化过程中，上题求得的点P与点C、D能否构成等腰三角形？若能够，求出所有符合条件的b值；若不能，试说明理由．

Answer 1

考点：反比例函数综合题

专题：

分析：（1）在y=-

1

2

x+

6

中，令x=0，解得y=

6

，求得B的坐标，令y=0求得A的坐标，则C的坐标即可求得；
（2）首先求得AP的解析式，然后解直线解析式与反比例函数的解析式组成的方程组即可求得P的坐标；
（3）若点P与点C、D能否构成等腰三角形，则CD=CP，首先求得C和D的坐标，根据CD=CP即可列方程求得b的值．

解答： 解：（1）在y=-

1

2

x+

6

中，令x=0，解得y=

6

，则B的坐标是（0，

6

）．
令y=0，解得：x=2

6

，则A的坐标是（2

6

，0）．
则C的坐标是（2

6

，

6

）．
把C代入y=

k

x

得：k=12．
则函数的解析式是：y=

12

x

；
（2）b=

5

2

时，直线y=-

1

2

x+

5

2

，令y=0，解得：x=5，
则A的坐标是（5，0）．
设AP的解析式是：y=2x+c，把（5，0）代入得：c=-10，
则直线AP的解析式是：y=2x-10．
解方程组

y=2x-10 y= 12 x

，
解得：

x=6 y=2

或

x=-1 y=-12

（舍去）．
则P的坐标是（6，2）；
（3）在y=-

1

2

x+b（b＞0）中，令x=0，解得y=b，则B的坐标是（0，b）．
令y=0，解得：x=2b，则A的坐标是（2b，0）．
故C的坐标是（2b，b），C的坐标是（b，b）．CD=b．
若点P与点C、D能否构成等腰三角形，则CD=CP．
即（6-2b）²+（2-b）²=b²，
解得：b=2或5．

点评：本题是二次函数与矩形的性质的综合应用，理解点P与点C、D能否构成等腰三角形，则CD=CP是关键．