题目内容
12.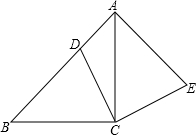 如图,在△ABC中,∠ACB=90°,AC=BC,点D是边AB上动点,(不与点A、点B重合),连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
如图,在△ABC中,∠ACB=90°,AC=BC,点D是边AB上动点,(不与点A、点B重合),连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.(1)求∠EAC的度数;
(2)求证:AD2+AE2=2CD2;
(3)若AB=2,在点D运动的过程中,四边形ADCE的周长和面积,一个是常量,一个是变量
①常量是面积,它的值是1
②变量是周长,求它的最小值.
分析 (1)先判断出△BCD≌△ACE,得出∠CAE=∠CBD,再根据等腰直角三角形的性质即可得出结论;
(2)构造直角三角形,利用勾股定理即可得出结论;
(3)由(1)的△BCD≌△ACE,得出四边形ADCE的面积等于△ABC的面积;再判断出AD+AE=2,进而判断出四边形ADCE的周长要最小,得出CD⊥AB即可得出结论.
解答 解:(1)由旋转知,CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=ACE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{BC=AC}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE,
∴∠CAE=∠CBD,
∵AC=BC,∠ACB=90°,
∴∠ABC=∠BAC=45°,
∴∠CAE=45°;
(2)如图,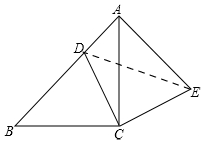
连接DE,
由(1)知,∠BAC=45°=∠CAE,
∴∠DAE=90°,根据勾股定理得,DE2=AD2+AE2,
由旋转知,∠DCE=90°,CD=CD,
∴DE2=2CD2,
∴AD2+AE2=2CD2;
(3)①
在Rt△ABC中,AC=BC,AB=2,
∴AC=BC=$\sqrt{2}$,
∴S△ABC=$\frac{1}{2}$AC×BC=1
由(1)知,△BCD≌△ACE,BD=AE,
∴S△BCD=S△ACE,
∴S四边形ADCE=S△ACE+S△ACD=S△BCD+S△ACD=S△ABC=1,
故答案为:面积,1;
②由①知,BD=AE,
∴AD+AE=AD+BD=AB=2,
由旋转知,CD=CE
∴L四边形ADCE=AD+AE+CE+CD=AB+2CD=2+2CD,
∴要四边形ADCE的周长最小,则CD最小,
∵点D在等腰直角三角形的斜边上,
∴CD⊥AB时,CD最小,最小值为$\frac{1}{2}$AB=1,
∴四边形ADCE的周长最小为2+2×1=4.
故答案为:周长.
点评 此题是四边形综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,勾股定理,解(1)的关键是判断出∠CAE=∠ABC,解(2)的关键是构造直角三角形,解(3)的关键是判断出四边形ADCE的面积是常量,周长是变量.

 阅读快车系列答案
阅读快车系列答案| A. | a=3,b=-5 | B. | a=3,b=1 | C. | a=-3,b=-1 | D. | a=-3,b=-5 |
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{\root{3}{3}}{4}$ | D. | $\frac{3}{4}$ |
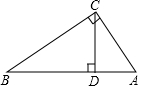 如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,其中AC=6,BC=8,AB=10,
如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,其中AC=6,BC=8,AB=10, 如图,把一张长方形纸条ABCD沿EF折叠,若∠1=53°,则∠AEG=74°.
如图,把一张长方形纸条ABCD沿EF折叠,若∠1=53°,则∠AEG=74°.