题目内容
1.请观察下列算式,再填空:32-12=8×1,52-32=8×2(1)①72-52=8×3; ②92-(7)2=8×4;
③(11)2+92=8×5; ④132-(11)2=8×6;
(2)通过观察,用一般形式表示出上述规律.
(3)请你运用所学知识,验证上述规律.
分析 (1)观察算式,补全空白;
(2)归纳总结得到一般性规律,写出即可;
(3)利用平方差公式证明即可.
解答 解:32-12=8×1
52-32=8×2
(1)①72-52=8×3;
②92-72=8×4;
③112-92=8×5;
④132-112=8×6;
(2)通过观察归纳,猜想第n个式子为(2n+1)2-(2n-1)2=8n;
(3)证明:(2n+1)2-(2n-1)2
=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]
=4n•2
=8n,得证.
故答案为:3;7,4;11;11,6.
点评 此题考查了因式分解的应用,规律型:数字的变化,平方差公式,找出题中的规律是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.一个等腰三角形的底角是40°,则它的顶角是( )
| A. | 40° | B. | 50° | C. | 80° | D. | 100° |
9.下列语句中,正确的是( )
| A. | 相等的角一定是对顶角 | |
| B. | 垂线最短 | |
| C. | 过一点有且只有一条直线与已知直线垂直 | |
| D. | 有一个公共顶点,且两边互为反向延长线的两个角是对顶角 |
13.北京地铁票价计费标准如表所示:
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.
小红妈妈上班时,需要乘坐地铁15公里到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第21次乘坐地铁上下班时,她刷卡支出的费用是( )
| 乘车距离x(公里) | x≤6 | 6<x≤12 | 12<x≤22 | 22<x≤32 | x>32 |
| 票价(元) | 3 | 4 | 5 | 6 | 每增加1元可乘坐20公里 |
小红妈妈上班时,需要乘坐地铁15公里到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第21次乘坐地铁上下班时,她刷卡支出的费用是( )
| A. | 2.5元 | B. | 3元 | C. | 4元 | D. | 5元 |
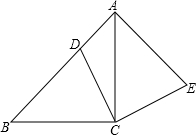 如图,在△ABC中,∠ACB=90°,AC=BC,点D是边AB上动点,(不与点A、点B重合),连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.
如图,在△ABC中,∠ACB=90°,AC=BC,点D是边AB上动点,(不与点A、点B重合),连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.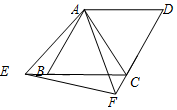 如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF.
如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF.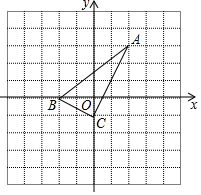 如图,直 角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)
如图,直 角坐标系中的网格由单位正方形构成,△ABC中,A点坐标为(2,3)