题目内容
如图，正方形ABCD中，DE=5，DF=3，求EK：EF的值．考点：正方形的性质,相似三角形的判定与性质
专题：
分析：过K作KM∥AD，交DC于M，先求得△KMD是等腰直角三角形，设KM=DM=x，根据KM∥AD，得出
=
=
，即可求得x的值，进而求得EK：EF的值．
| KM |
| DF |
| EM |
| DE |
| EK |
| EF |
解答：
解：如图，过K作KM∥AD，交DC于M，
∵正方形ABCD中，BD是对角线，
∴∠BDC=45°，
∴△KMD是等腰直角三角形，
∴KM=DM，
设KM=DM=x，
∵KM∥AD，
∴△KME∽△FDE，
∴
=
=
即
=
，
解得x=
．
∴
=
=
．
解：如图，过K作KM∥AD，交DC于M，∵正方形ABCD中，BD是对角线，
∴∠BDC=45°，
∴△KMD是等腰直角三角形，
∴KM=DM，
设KM=DM=x，
∵KM∥AD，
∴△KME∽△FDE，
∴
| KM |
| DF |
| EM |
| DE |
| EK |
| EF |
即
| x |
| 3 |
| 5-x |
| 5 |
解得x=
| 15 |
| 8 |
∴
| EK |
| EF |
| x |
| 3 |
| ||
| 3 |
| 5 |
| 8 |
点评：本题考查了正方形的性质，等腰直角三角形的判定和性质，三角形相似判定和性质，作出辅助线构建相似三角形是本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
已知，M是△ABC内的一点，MD⊥BC，ME⊥AC，MF⊥AB，且BD=BF，CD=CE，求证：AE=AF．
我国是世界上严重缺水的国家之一，为了增强居民的节水意识，某自来水公司对居民用水采取以户为单位分段计费办法收费：即每月用水10吨以内（包括10吨）的用户，每吨水收费a元，每月用水超过10吨的部分，按每吨b元（b＞a）收费，设一户居民月用水x（吨），应收水费y（元），y与x之间的函数关系如图所示．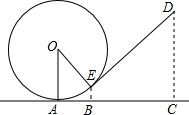
如图是小朋友玩的“滚铁环”游戏的示意图，⊙O向前滚动时，铁棒DE保持与OE垂直．⊙O与地面接触点为A，若⊙O的半径为25cm，cos∠AOE=