题目内容
已知直线y=-
x+3与x轴、y轴分别交于A、B两点,点C(n,O)是x轴上一点,把坐标平面沿直线BC折叠,使点A刚好落在y轴上,则点C的坐标是 .
| 3 |
| 4 |
考点:翻折变换(折叠问题),一次函数图象上点的坐标特征
专题:
分析:令y=0求出OA,令x=0求出OB,利用勾股定理列式求出AB,再根据翻折变换的性质可得A′B=AB,A′C=AC,根据点C的坐标表示出AC,然后利用勾股定理列方程求解即可.
解答: 解:令y=0,则-
解:令y=0,则-
x+3=0,
解得x=4,
所以,OA=4,
令x=0,则y=3,
所以,OB=3,
由勾股定理得,AB=
=
=5,
如图,坐标平面沿直线BC折叠点A落在y轴上点A′处,
则A′B=AB,A′C=AC,
∴OA′=A′B-OB=5-3=2,
∵点C(n,0),
∴OC=n,A′C=AC=4-n,
在Rt△A′OC中,OA′2+OC2=A′C2,
即22+n2=(4-n)2,
解得n=
,
所以,点C的坐标为(
,0).
故答案为:(
,0).
 解:令y=0,则-
解:令y=0,则-| 3 |
| 4 |
解得x=4,
所以,OA=4,
令x=0,则y=3,
所以,OB=3,
由勾股定理得,AB=
| OA2+OB2 |
| 42+32 |
如图,坐标平面沿直线BC折叠点A落在y轴上点A′处,
则A′B=AB,A′C=AC,
∴OA′=A′B-OB=5-3=2,
∵点C(n,0),
∴OC=n,A′C=AC=4-n,
在Rt△A′OC中,OA′2+OC2=A′C2,
即22+n2=(4-n)2,
解得n=
| 3 |
| 2 |
所以,点C的坐标为(
| 3 |
| 2 |
故答案为:(
| 3 |
| 2 |
点评:本题考查了翻折变换的性质,勾股定理,熟记性质并利用勾股定理列出方程是解题的关键,作出图形更形象直观.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图的坐标平面上有一正五边形ABCDE,其中C、D两点坐标分别为(1,0)、(2,0).若在没有滑动的情况下,将此正五边形沿着x轴向右滚动,则滚动过程中,下列哪个点会经过点(76,0)?( )
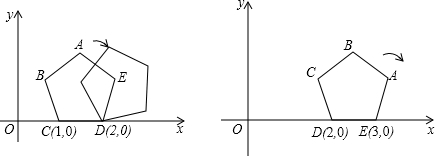

| A、A | B、B | C、C | D、D |
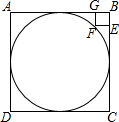 圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )
圆与正方形ABCD内切,BEFG为边长1的正方形.求正方形ABCD的边长( )A、4+2
| ||
| B、2π | ||
C、5
| ||
D、
| ||
E、4
|
 如图,正方形ABCD中,DE=5,DF=3,求EK:EF的值.
如图,正方形ABCD中,DE=5,DF=3,求EK:EF的值.