题目内容
14. 如图,点A在双曲线y=$\frac{k}{x}$的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点D为OB的中点,若△ADC的面积为4,则k的值为$\frac{16}{3}$.
如图,点A在双曲线y=$\frac{k}{x}$的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点D为OB的中点,若△ADC的面积为4,则k的值为$\frac{16}{3}$.
分析 设A点坐标为(a,b),则k=ab,AB=a,OC=2AB=2a,BD=OD=$\frac{1}{2}$b,利用S梯形OBAC=S△ABD+S△ADC+S△ODC得$\frac{1}{2}$(a+2a)×b=$\frac{1}{2}$a×$\frac{1}{2}$b+4+$\frac{1}{2}$×2a×$\frac{1}{2}$b,整理可得ab=$\frac{16}{3}$,即可得到k的值.
解答 设A点坐标为(a,b),则AB=a,OC=2AB=2a,
而点D为OB的中点,
∴BD=OD=$\frac{1}{2}$b,
∵S梯形OBAC=S△ABD+S△ADC+S△ODC,
∴$\frac{1}{2}$(a+2a)×b=$\frac{1}{2}$a×$\frac{1}{2}$b+4+$\frac{1}{2}$×2a×$\frac{1}{2}$b,
∴ab=$\frac{16}{3}$,
把A(a,b)代入双曲线y=$\frac{k}{x}$,
∴k=ab=$\frac{16}{3}$.
故答案为:$\frac{16}{3}$.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数图象上点的坐标特征.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
4.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 等腰直角三角形 | B. | 平行四边形 | C. | 圆 | D. | 等边三角形 |
6.若$\frac{3a+1}{(a+3)(a-1)}$=$\frac{m}{a+3}$+$\frac{n}{a-1}$,则( )
| A. | m=-3,n=1 | B. | m=3,n=-1 | C. | m=3,n=1 | D. | m=2,n=1 |
4. 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
 某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )
某校共有2425名学生,其中各年级学生所占比例如扇形统计图,则学生最多的年级有( )| A. | 873名 | B. | 1115名 | C. | 485名 | D. | 1067名 |
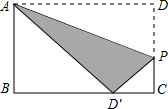 如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由点D向点C运动,沿直线AP翻折三角形ADP,使点D恰好落在BC边上.求DP的长和三角形ADP与矩形重叠(阴影)部分的面积.
如图,矩形ABCD中,AB=8,BC=10,点P在矩形的边DC上由点D向点C运动,沿直线AP翻折三角形ADP,使点D恰好落在BC边上.求DP的长和三角形ADP与矩形重叠(阴影)部分的面积.