题目内容
等边△ABC的边长为1,点E、F分别在边AB、AC上,沿EF将AEF翻折,使点A恰好落在BC上的点D,已知AE:AF=5:4,求BD长.
考点:翻折变换(折叠问题),等边三角形的性质
专题:
分析:首先根据题意作出图形,根据翻折变换的性质及相似三角形的判定定理来证明△BDE∽△CFD,进而找出BD、CF之间的数量关系;利用余弦定理求出线段BD的长.
解答: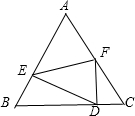 解:如图,由题意得:△AEF≌△DEF,
解:如图,由题意得:△AEF≌△DEF,
∴DE=AE,DF=AF;∠EDF=∠A;
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°;
∴∠EDF=∠B=∠C=60°;
∴∠BED+∠BDE=∠CDF+∠BDE=180°-60°=120°,
∴∠BED=∠CDF;
又∵∠B=∠C,
∴△BDE∽△CFD,
∴
=
;
又∵DE=AE,DF=AF,且AE:AF=5:4,
∴BD:CF=5:4;
设BD=5m,则CF=4m,
∴CD=1-5m,DF=AF=1-4m;
由勾股定理得:
DF2=CD2+CF2-2CD•CF•cos60°,
即(1-4m)2=(1-5m)2+(4m)2-2(1-5m)(4m)×
,
整理得:45m2-6m=0,
解得:m=
或m=0(舍去);
∴BD的长为
.
 解:如图,由题意得:△AEF≌△DEF,
解:如图,由题意得:△AEF≌△DEF,∴DE=AE,DF=AF;∠EDF=∠A;
∵△ABC为等边三角形,
∴∠A=∠B=∠C=60°;
∴∠EDF=∠B=∠C=60°;
∴∠BED+∠BDE=∠CDF+∠BDE=180°-60°=120°,
∴∠BED=∠CDF;
又∵∠B=∠C,
∴△BDE∽△CFD,
∴
| BD |
| CF |
| DE |
| DF |
又∵DE=AE,DF=AF,且AE:AF=5:4,
∴BD:CF=5:4;
设BD=5m,则CF=4m,
∴CD=1-5m,DF=AF=1-4m;
由勾股定理得:
DF2=CD2+CF2-2CD•CF•cos60°,
即(1-4m)2=(1-5m)2+(4m)2-2(1-5m)(4m)×
| 1 |
| 2 |
整理得:45m2-6m=0,
解得:m=
| 2 |
| 15 |
∴BD的长为
| 2 |
| 3 |
点评:该命题以等边三角形为载体,以翻折变换为手段,以考查相似三角形的判定及其性质的应用为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
 已知⊙O的半径为5,△ABC是⊙O的内接三角形,AD是△ABC的高,且AC=4.
已知⊙O的半径为5,△ABC是⊙O的内接三角形,AD是△ABC的高,且AC=4. 如图,在矩形ABCD中,把点B沿AF对折,使点B落在CD边上的E点,若AB=10,AC=8,求FE的长.
如图,在矩形ABCD中,把点B沿AF对折,使点B落在CD边上的E点,若AB=10,AC=8,求FE的长.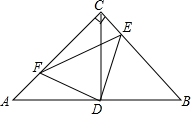 如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD
如图,在等腰Rt△ABC中,∠ACB=90°,D是AB边上的中点,点E、F分别在BC、AC边上运动,且保持AF=CE,连接DE,DF,EF,CD