题目内容
5. 如图,反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A(2,2),B($\frac{1}{2}$,n).
如图,反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于点A(2,2),B($\frac{1}{2}$,n).(1)求这两个函数解析式;
(2)根据图象直接回答:在第一象限内,当x满足条件$\frac{1}{2}$<x<2时,一次函数大于反比例函数的值;
(3)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y=$\frac{k}{x}$的图象有且只有一个交点,求m的值.
分析 (1)利用待定系数法求两函数的解析式;
(2)由图象得出;
(3)列方程组,一个交点则△=0,可得结论.
解答 解:(1)把点A(2,2)代入反比例函数y=$\frac{k}{x}$中,
得:k=2×2=4,
∴反比例函数解析式为:y=$\frac{4}{x}$,
当x=$\frac{1}{2}$时,$\frac{1}{2}$n=4,
n=8,
∴B($\frac{1}{2}$,8),
则$\left\{\begin{array}{l}{2a+b=2}\\{\frac{1}{2}a+b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-4}\\{b=10}\end{array}\right.$,
∴一次函数的解析式为:y=-4x+10;
(2)由图象得:当$\frac{1}{2}$<x<2时,一次函数大于反比例函数的值;
故答案为:$\frac{1}{2}$<x<2;
(3)设平移后的解析式为y=-4x+10-m与y=$\frac{4}{x}$图象只有一个交点,
则$\left\{\begin{array}{l}{y=-4x+10-m}\\{y=\frac{4}{x}}\end{array}\right.$,
得:4x2+(m-10)x+4=0,
∴△=(m-10)2-4×4×4=0,
解得:m=2或18.
点评 本题考查了利用待定系数法求函数的解析式、反比例函数与一次函数的交点问题,熟练掌握两函数的交点即是两函数解析式所列方程组的解,也可以利用根的判别式判断交点的个数.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
15. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在点D′,C′的位置,若∠EFB=70°,则∠AED′等于( )| A. | 40° | B. | 50° | C. | 65° | D. | 70° |
16.x为任意实数时,下列分式一定有意义的是( )
| A. | $\frac{x+5}{{x}^{2}}$ | B. | $\frac{x-1}{{x}^{3}+1}$ | C. | $\frac{x+1}{{x}^{2}-9}$ | D. | $\frac{x+1}{|x|+1}$ |
10.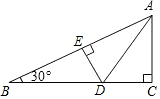 如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )
如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )
 如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )
如图,∠ACB=90°,∠ABC=30°,AD平分∠BAC,DE⊥AB,DE=2.5cm,AC=4cm,则△ABC的周长为( )| A. | 19.5cm | B. | 20cm | C. | 20.5cm | D. | 19cm |
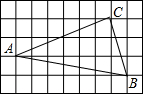 如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.
如图,在9×5的正方形网格中,每个小正方形边长均为1,△ABC的顶点均在格点上.