题目内容
18.解不等式(组)并把解集在数轴上表示:(1)2-5x≥8-2x
(2)$\left\{\begin{array}{l}3x+2≥5x-6\\ 3-2x≥2+x\end{array}\right.$.
分析 (1)先移项、合并得到-3x≥6,然后把x的系数化为1即可得到不等式的解集,再利用数轴表示解集;
(2)分别解两个不等式得到x≤4和x≤$\frac{1}{3}$,然后根据确定不等式组的解集,再利用数轴表示解集.
解答 解:(1)移项得-5x+2x≥8-2,
合并同类项得-3x≥6,
系数化为1得x≤-2,
用数轴表示为:
(2)$\left\{\begin{array}{l}{3x+2≥5x-6①}\\{3-2x≥2+x②}\end{array}\right.$,
解①得x≤4,
解②得x≤$\frac{1}{3}$,
所以不等式组的解集为x≤$\frac{1}{3}$,
用数轴表示为:
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.也考查了一元一次不等式和用数轴表示不等式的解集.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
10.“快乐购”超市购进一批20元/千克的绿色食品,如果以30元/千克销售,那么每天可售出400千克.由销售经验知,每天销售量y(千克)与销售单价x(元)(x≥30)成一次函数关系,部分对应值如下表.
(1)试求出y与x的函数关系式;
(2)设“快乐购”超市销售该绿色食品每天获得利润P元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出答案).
| x(元) | 30 | 31 | 32 | 33 | 34 | 35 | … |
| y(千克) | 400 | 380 | 360 | 340 | 320 | 300 | … |
(2)设“快乐购”超市销售该绿色食品每天获得利润P元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过4480元,现该超市经理要求每天利润不得低于4180元,请你帮助该超市确定绿色食品销售单价x的范围(直接写出答案).
8.如果|a|=2,b的相反数是1,那么|a+b|的值为( )
| A. | 1 | B. | 3 | C. | 1或3 | D. | -1或-3 |
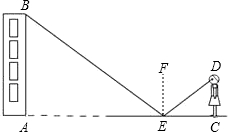 小强用这样的方法来测量学校教学楼的高度:如图,在地面上放一面镜子(镜子高度忽略不计),他刚好能从镜子中看到教学楼的顶端B,他请同学协助量了镜子与教学楼的距离EA=21米,以及他与镜子的距离CE=2.5米,已知他的眼睛距离地面的高度DC=1.6米,请你帮助小强计算出教学楼的高度.(根据光的反射定律:反射角等于入射角)
小强用这样的方法来测量学校教学楼的高度:如图,在地面上放一面镜子(镜子高度忽略不计),他刚好能从镜子中看到教学楼的顶端B,他请同学协助量了镜子与教学楼的距离EA=21米,以及他与镜子的距离CE=2.5米,已知他的眼睛距离地面的高度DC=1.6米,请你帮助小强计算出教学楼的高度.(根据光的反射定律:反射角等于入射角) 公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB=15m,AD=12m,AC⊥BC,求小路BC的长,并算出绿地的面积.
公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB=15m,AD=12m,AC⊥BC,求小路BC的长,并算出绿地的面积.