题目内容
8.(1)已知a=3+2$\sqrt{2}$,b=3-2$\sqrt{2}$.求a2b-ab2的值.(2)当x=$\sqrt{24}$-1时,求x2+2x+2的值.
分析 (1)首先将原式提取公因式进而分解因式将已知代入求出即可;
(2)将原式利用完全平方公式将原式变形进而代入已知求出即可.
解答 解:(1)∵a=3+2$\sqrt{2}$,b=3-2$\sqrt{2}$,
∴a2b-ab2
=ab(a-b)
=(3+2$\sqrt{2}$)(3-2$\sqrt{2}$)(3+2$\sqrt{2}$-3+2$\sqrt{2}$)
=(9-8)×4$\sqrt{2}$
=4$\sqrt{2}$;
(2)∵x=$\sqrt{24}$-1,
∴x2+2x+2=(x+1)2+1=(2$\sqrt{6}$-1+1)2+1=24+1=25.
点评 此题主要考查了二次根式的化简求值,正确分解因式是解题关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
20.不等式2x+5>3的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
17.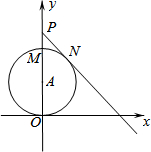 如图,直角坐标系中,P点坐标为(0,4),M为线段OP上(不含O、P)一动点,以OM为直径作⊙A,PN切⊙A于N,设PN-PM=m,则m的值( )
如图,直角坐标系中,P点坐标为(0,4),M为线段OP上(不含O、P)一动点,以OM为直径作⊙A,PN切⊙A于N,设PN-PM=m,则m的值( )
 如图,直角坐标系中,P点坐标为(0,4),M为线段OP上(不含O、P)一动点,以OM为直径作⊙A,PN切⊙A于N,设PN-PM=m,则m的值( )
如图,直角坐标系中,P点坐标为(0,4),M为线段OP上(不含O、P)一动点,以OM为直径作⊙A,PN切⊙A于N,设PN-PM=m,则m的值( )| A. | 为定值1 | B. | 0<m≤1 | C. | 0<m≤2 | D. | $\frac{1}{2}$≤m≤1 |
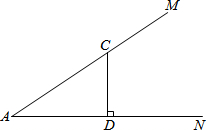 如图,点C在∠MAN的边AM上,CD⊥AN,垂足为点D,点B在边AN上运动,∠BCA的平分线交AN于点E.
如图,点C在∠MAN的边AM上,CD⊥AN,垂足为点D,点B在边AN上运动,∠BCA的平分线交AN于点E.