题目内容
14.解下列方程:(1)$\frac{x-1}{x+1}$+$\frac{2x}{1-2x}$=0;
(2)$\frac{x}{x-3}$-2=$\frac{4}{x-3}$;
(3)$\frac{2x}{x+2}$-$\frac{3}{x-2}$=2;
(4)$\frac{7}{{x}^{2}+x}$-$\frac{3}{x-{x}^{2}}$=1+$\frac{7-{x}^{2}}{{x}^{2}-1}$;
(5)$\frac{5x-4}{2x-4}$=$\frac{2x+5}{3x-2}$-$\frac{1}{2}$;
(6)$\frac{1}{x+1}$+$\frac{1}{x+5}$=$\frac{1}{x+2}$+$\frac{1}{x+4}$.
分析 各分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:(x-1)(1-2x)+2x(x+1)=0,
整理得:x-1+2x+2x=0,
解得:x=$\frac{1}{5}$,
经检验x=$\frac{1}{5}$是分式方程的解;
(2)去分母得:x-2x+6=4,
解得:x=2,
经检验x=2是分式方程的解;
(3)去分母得:2x(x-2)-3(x+2)=2x2-8,
解得:x=$\frac{2}{7}$,
经检验x=$\frac{2}{7}$是分式方程的解;
(4)去分母得:7x-7+3x+3=x(x2-1)+7x-x3,
移项合并得:4x=4,
解得:x=1,
经检验x=1是增根,分式方程无解;
(5)去分母得:2(5x-4)(3x-2)=2(2x+5)(2x-4)-(2x-4)(3x-2),
整理得:7x2-16x+16=0,
∵△<0,
则分式方程无解;
(6)通分得:$\frac{2x+6}{{x}^{2}+6x+5}$=$\frac{2x+6}{{x}^{2}+6x+8}$,
整理得:x2+6x+5=x2+6x+8,即5=8,
则分式方程无解.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
相关题目
4.由下列三条线段组成的三角形不是直角三角形的是( )
| A. | $\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$ | B. | 0.9,1.2,1.5 | C. | $\sqrt{2}$,$\sqrt{3}$,$\sqrt{5}$ | D. | $\sqrt{41}$,4,5 |
5.已知甲、乙、丙、丁共有30本,又知甲、乙、丙、丁的课外书制作的条形统计图的高度之比为2:3:4:1,则乙的课外书的本数为( )
| A. | 6本 | B. | 9本 | C. | 11本 | D. | 12本 |
9. 如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )
 如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=46°,∠CEF=160°,则∠BCE等于( )| A. | 26° | B. | 16° | C. | 23° | D. | 20° |
3.甲,乙两人分别骑车从A,B两地相向而行,甲先行1小时后,乙才出发,又经过4小时两人在途中的C地相遇.相遇后两人按原来的方向继续前进,乙在由C地到达A地的途中因故障停了20分钟,结果乙由C地到达A地比甲由C地到达B地还提前了40分钟.已知乙比甲每小时多行驶4千米,则甲、乙两人骑车的速度分别为( )千米/时.
| A. | 2,6 | B. | 12,16 | C. | 16,20 | D. | 20,24 |
15.若$\sqrt{x-1}$的在实数范围内有意义,则( )
| A. | x≥1 | B. | x≠1 | C. | x>1 | D. | x≤1 |
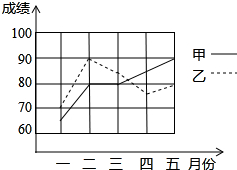 为了从甲,乙两名学生中选拔一人参加竞赛,学校每个月对他们的学习进行了一次测验,如图是两人赛前5次测验成绩的折线统计图.(每次测试的成绩均为5的倍数)
为了从甲,乙两名学生中选拔一人参加竞赛,学校每个月对他们的学习进行了一次测验,如图是两人赛前5次测验成绩的折线统计图.(每次测试的成绩均为5的倍数)