题目内容
6.已知a、b、c分别为△ABC的三边长,且a2+b2=c2,△ABC是直角三角形吗?为什么?分析 作Rt△A′B′C′,使∠C′=90°,B′C′=BC=a,A′C′=AC=b,由勾股定理求出A′B′=AB,再根据SSS证明△ABC≌△A′B′C′,由全等三角形的对应角相等即可得出∠C=∠C′=90°.
解答 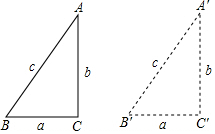 证明:作Rt△A′B′C′,使∠C′=90°,B′C′=BC=a,A′C′=AC=b,
证明:作Rt△A′B′C′,使∠C′=90°,B′C′=BC=a,A′C′=AC=b,
由勾股定理,得A′B′2=B′C′2+A′C′2=a2+b2,
∵a2+b2=c2,AB=c,
∴A′B′2=AB2,
∴A′B′=AB.
在△ABC与△A′B′C′中,
$\left\{\begin{array}{l}{BC=B′C′}\\{AC=A′C′}\\{AB=A′B′}\end{array}\right.$,
∴△ABC≌△A′B′C′(SSS),
∴∠C=∠C′=90°,
即△ABC是直角三角形.
点评 本题考查了勾股定理逆定理的证明,其中涉及到勾股定理,全等三角形的判定与性质,作辅助线构造直角三角形是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14.下列由左到右的变形中,不属于因式分解的是( )
| A. | x(x-2)+1=(x-1)2 | B. | a2b+ab3=ab(a+b2) | ||
| C. | x2+2xy+1=x(x+2y)+1 | D. | a2b2-1=(ab+1)(ab-1) |
1.下列根式中,不是二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{4}$ | C. | $\sqrt{{a}^{2}}$ | D. | $\sqrt{-3}$ |
18.A、B两个动点在数轴上做匀速运动,它们的运动时间以及位置记录如表.
(1)根据题意,填写下列表格;
(2)A、B两点能否相遇,如果相遇,求相遇时的时刻及在数轴上的位置;如果不能相遇,请说明理由;
(3)A、B两点能否相距9个单位长度?如果能,求相距9个单位长度的时刻;如不能,请说明理由.
(1)根据题意,填写下列表格;
| 时间(秒) | 0 | 5 | 7 |
| A点位置 | 19 | -1 | -9 |
| B点位置 | -8 | 17 | 27 |
(3)A、B两点能否相距9个单位长度?如果能,求相距9个单位长度的时刻;如不能,请说明理由.
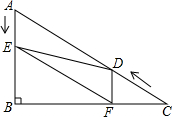 如图所示,在直角△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE,EF.
如图所示,在直角△ABC中,∠B=90°,BC=5$\sqrt{3}$,∠C=30°,点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE,EF.