题目内容
一个凸多边形共有20条对角线,它是几边形?是否存在有18条对角线的多边形?如果存在,它是几边形?如果不存在,说明得出结论的道理.
考点:多边形的对角线
专题:
分析:利用多边形对角线条数求法得出即可.
解答:解:设这个多边形是n边形,则
∵
=20,
∴n2-3n-40=0,
(n-8)(n+5)=0,
解得n=8,n=-5(舍去),
故多边形的边数为8;
∵
=18,
∴n2-3n-36=0,
∵b2-4ac=9+144=153,
∴方程的根,无法求出整数,
故这样的多边形不存在.
∵
| n(n-3) |
| 2 |
∴n2-3n-40=0,
(n-8)(n+5)=0,
解得n=8,n=-5(舍去),
故多边形的边数为8;
∵
| n(n-3) |
| 2 |
∴n2-3n-36=0,
∵b2-4ac=9+144=153,
∴方程的根,无法求出整数,
故这样的多边形不存在.
点评:此题主要考查了多边形对角线公式,熟练记忆公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为30m.
如图,为了求河的宽度,在河对岸岸边任意取一点A,再在河这边沿河边取两点B、C,使得∠ABC=60°,∠ACB=45°,量得BC长为30m.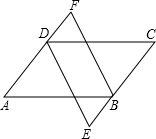 如图,在平行四边形ABCD中,DE平分∠ADC,交CB延长线于点E,BF平分∠ABC,交AD延长线于点F.求证:四边形BFDE是平行四边形.
如图,在平行四边形ABCD中,DE平分∠ADC,交CB延长线于点E,BF平分∠ABC,交AD延长线于点F.求证:四边形BFDE是平行四边形.