题目内容
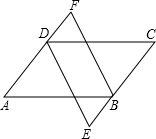 如图,在平行四边形ABCD中,DE平分∠ADC,交CB延长线于点E,BF平分∠ABC,交AD延长线于点F.求证:四边形BFDE是平行四边形.
如图,在平行四边形ABCD中,DE平分∠ADC,交CB延长线于点E,BF平分∠ABC,交AD延长线于点F.求证:四边形BFDE是平行四边形.考点:平行四边形的判定与性质
专题:证明题
分析:首先证明∠CDE=∠ABF,再证明ED∥FB,然后再根据平行四边形的性质可得AF∥CE,根据两组对边分别平行的四边形是平行四边形可得四边形BFDE是平行四边形.
解答: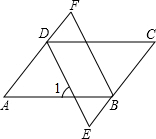 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,
∴∠ADC=∠ABC,DC∥AB,AD∥BC,
∵DE平分∠ADC,
∴∠CDE=
∠ADC,
∵BF平分∠ABC,
∴∠ABF=
∠ABC,
∴∠CDE=∠ABF,
∵DC∥AB,
∴∠1=∠CDE,
∴∠1=∠FBA,
∴ED∥FB,
∵AF∥CE,
∴四边形BFDE是平行四边形.
 证明:∵四边形ABCD是平行四边形,
证明:∵四边形ABCD是平行四边形,∴∠ADC=∠ABC,DC∥AB,AD∥BC,
∵DE平分∠ADC,
∴∠CDE=
| 1 |
| 2 |
∵BF平分∠ABC,
∴∠ABF=
| 1 |
| 2 |
∴∠CDE=∠ABF,
∵DC∥AB,
∴∠1=∠CDE,
∴∠1=∠FBA,
∴ED∥FB,
∵AF∥CE,
∴四边形BFDE是平行四边形.
点评:此题主要考查了平行四边形的性质和判定,关键是掌握平行四边形两组对边分别平行,两组对边分别平行的四边形是平行四边形.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于F,试探究∠DEF与∠B,∠C的数量关系.
在△ABC中,∠1=∠2,∠C>∠B,E为AD上一点,且EF⊥BC于F,试探究∠DEF与∠B,∠C的数量关系. 已知:AB∥CD,AD∥BC.求证:OA=OC,OB=OD.
已知:AB∥CD,AD∥BC.求证:OA=OC,OB=OD.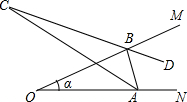 如图,已知∠MON=α,点A、B分别在射线ON、OM上移动(不与点O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若改变,说明理由;若不改变,求出其值.
如图,已知∠MON=α,点A、B分别在射线ON、OM上移动(不与点O重合),AC平分∠OAB,BD平分∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ABM,直线AC、BD交于点C.试问:随着A、B点的移动变化,∠ACB的大小是否也随之变化?若改变,说明理由;若不改变,求出其值.