题目内容

5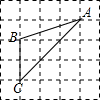．如图，已知△ABC的三个顶点均在格点上，则cosA的值为$\frac{2\sqrt{5}}{5}$．

分析 连接BD，根据勾股定理的逆定理判断出△ABD的形状，再由锐角三角函数的定义即可得出结论．

解答 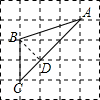解：连接BD，
∵BD2=12+12=2，AB2=12+32=10，AD2=22+22=8，2+8=10，
∴△ABD是直角三角形，且∠ADB=90°，
∴cosA=$\frac{AD}{AB}$=$\frac{\sqrt{8}}{\sqrt{10}}$=$\frac{4\sqrt{5}}{10}$=$\frac{2\sqrt{5}}{5}$．
故答案为：$\frac{2\sqrt{5}}{5}$．

点评 本题主要考查了锐角三角函数和勾股定理，作出适当的辅助线构建直角三角形是解答此题的关键．

练习册系列答案
相关题目
15．要使$\frac{x-1}{x-3}$有意义，则x的取值范围是（　　）
A．x≠1B．x≠3C．x≥1且x≠3D．x≥3且x≠1
16．在学习三视图时，老师在讲台上用四盒粉笔盒摆放出如图形状的几何体，那么该几何体的左视图正确的是（　　）
A．B．C．D．
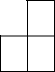
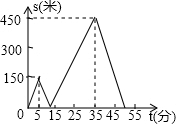13．甲、乙两人匀速行走从同一地点到距离1500米处的图书馆，甲出发5分钟后，乙出发并沿同一路线行走，乙的速度是甲的速度的$\frac{5}{3}$．设甲、乙两人相距s（米），甲行走的时间为t（分），s关于t的函数图象如图所示，下列说法
①甲行走的速度是30米/分，乙的速度是50米/分；
②乙走了7.5分钟就追上了甲；        
③当甲、乙两人到达图书馆时分别用了50分钟和35分钟；
④甲行走30.5分钟或38分钟时，甲、乙两人相距360米；
其中正确的个数是（　　）
A．1个B．2个C．3个D．4个
20．如图，A（2，1），B（1，-1），以O为位似中心，按比例尺1：2，把△AOB放大，则点A的对应点A′的坐标为（4，2）或（-4，-2）．
10．（1）问题发现：
如图1，在边长为4的正方形ABCD中，点E、F分别是边CD、AD上的动点，连接BE、CF交于点P，若始终保持CE=DF．
①线段BE和CF的关系是 BE=CF，且BE⊥CF，说明理由；
②当点E从点C运动到点D时，求点P运动的路径长；
（2）拓展探究：
如图2，在边长为6的等边三角形ABC中，点E、F分别是边AC、BC上的动点，连接AF、BE，交于点P，若始终保持AE=CF，当点E从点A运动到点C时，直接写出点P运动的路径长是 $\frac{4\sqrt{3}}{3}$π．
17．如图1，在平面直角坐标系xOy中，A，B两点的坐标分别为A（x1，y1），B（x2，y2），由勾股定理得AB2=|x2-x1|2+|y2-y1|2，所以A，B两点间的距离为．AB=$\sqrt{|{x}_{1}-{x}_{2}{|}^{2}+|{y}_{1}-{y}_{2}{|}^{2}}$．
我们知道，圆可以看成到圆心距离等于半径的点的集合，如图2，在平面直角坐标系xOy中，A（x，y）为圆上任意一点，则A到原点的距离的平方为OA2=|x-0|2+|y-0|2，当⊙O的半径为r时，⊙O的方程可写为：x2+y2=r2．
（1）问题拓展：
如果圆心坐标为P（a，b），半径为r，那么⊙P的方程可以写为（x-a）2+（y-b）2=r2．
（2）综合应用：
如图3，⊙P与x轴相切于原点O，P点坐标为（0，6），A是⊙P上一点，连接OA，使tan∠POA=$\frac{3}{4}$，作PD⊥OA，垂足为D，延长PD交x轴于点B，连结AB．
①证明AB是⊙P的切线；
②是否存在到四点O，P，A，B距离都相等的点Q？若存在，求Q点坐标，并写
出以Q为圆心，以OQ为半径的⊙Q的方程；若不存在，说明理由．
14．若抛物线y=ax2+bx+c如图所示，下列四个结论：
①abc＜0；②b-2a＜0；③a-b+c＜0；④b2-4ac＞0．
其中正确结论的个数是（　　）
A．1B．2C．3D．4
15．在平面直角坐标系中，已知点A（-1，2），则点A关于x轴的对称点B的坐标是（　　）
A．（-1，-2）B．（1，2）C．（2，-1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网